题目内容
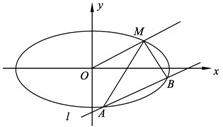 如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1)平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.
如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1)平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)求证:直线MA、MB与x轴始终围成一个等腰三角形.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:( I)设椭圆的方程为
+
=1(a>b>0),由题可得
,由此能求出椭圆的方程.
( II)直线l方程为:y=
x+m.联立
,得2x2+6mx+9m2-18=0,由此能求出m的取值范围.
( III)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0,就能得到直线MA、MB与x轴围成一个等腰三角形.
| x2 |
| a2 |
| y2 |
| b2 |
|
( II)直线l方程为:y=
| 1 |
| 3 |
|
( III)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0,就能得到直线MA、MB与x轴围成一个等腰三角形.
解答:
 ( I)解:设椭圆的方程为
( I)解:设椭圆的方程为
+
=1(a>b>0)
由题可得
,解得a2=18,b2=2.
所求椭圆的方程为
+
=1.…(4分)
( II)解:∵直线l∥OM且在y轴上的截距为m,
∴直线l方程为:y=
x+m.
联立
消y化简得2x2+6mx+9m2-18=0
∵直线l交椭圆于A,B两点,
∴△=(6m)2-4×2×(9m2-18)>0
解得-2<m<2又因为m≠0.
∴m的取值范围为-2<m<2且m≠0.…(8分)
( III)证明:设直线MA、MB的斜率分别为k1,k2,
则问题只需证明k1+k2=0.
设A(x1,y1),B(x2,y2)则k1=
,k2=
.
由(2)x1+x2=-3m,x1•x2=
又y1=
x1+m,y2=
x2+m,
代入k1+k2=
,整理得:
∴k1+k2=0.从而直线MA、MB与x轴围成一个等腰三角形.…(13分)
 ( I)解:设椭圆的方程为
( I)解:设椭圆的方程为| x2 |
| a2 |
| y2 |
| b2 |
由题可得
|
所求椭圆的方程为
| x2 |
| 18 |
| y2 |
| 2 |
( II)解:∵直线l∥OM且在y轴上的截距为m,
∴直线l方程为:y=
| 1 |
| 3 |
联立
|
消y化简得2x2+6mx+9m2-18=0
∵直线l交椭圆于A,B两点,
∴△=(6m)2-4×2×(9m2-18)>0
解得-2<m<2又因为m≠0.
∴m的取值范围为-2<m<2且m≠0.…(8分)
( III)证明:设直线MA、MB的斜率分别为k1,k2,
则问题只需证明k1+k2=0.
设A(x1,y1),B(x2,y2)则k1=
| y1-1 |
| x1-3 |
| y2-1 |
| x2-3 |
由(2)x1+x2=-3m,x1•x2=
| 9m2-18 |
| 2 |
又y1=
| 1 |
| 3 |
| 1 |
| 3 |
代入k1+k2=
| (y1-1)(x2-3)+(y2-1)(x1-3) |
| (x1-3)(x2-3) |
|
∴k1+k2=0.从而直线MA、MB与x轴围成一个等腰三角形.…(13分)
点评:本题考查椭圆方程的求法,考查实数的取值范围的求法,考查等腰三角形的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x3-x2+1,则f(x)在点(1,1)处的切线的倾斜角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
“所有9的倍数都是3的倍数.某数是9的倍数,故该数为3的倍数,”上述推理( )
| A、完全正确 |
| B、推理形式不正确 |
| C、错误,因为大小前提不一致 |
| D、错误,因为大前提错误 |
用反证法证明命题“自然数a,b,c中三个均为偶数”的反设( )
| A、全是奇数 |
| B、恰有一个偶数 |
| C、至少有一个偶数 |
| D、至多有两个偶数 |
若球的表面积扩大到原来的2倍,则球的体积扩大到原来的( )
| A、2倍; | ||
B、
| ||
C、2
| ||
D、3
|
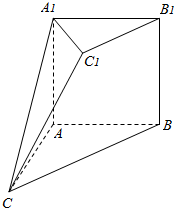 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=