题目内容
已知点Q（0，2
）及抛物线y2=4x上一动点P（x，y），则x+|PQ|的最小值是（ ）
| 2 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、2
|
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设抛物线的焦点为F（1，0），则由抛物线的定义，可得x+|PQ|的最小值是|QF|-1．
解答：
解：设抛物线的焦点为F（1，0），则由抛物线的定义，可得x+|PQ|的最小值是|QF|-1，
∵点Q（0，2
），
∴x+|PQ|的最小值是|QF|-1=3-1=2，
故选：A．
∵点Q（0，2
| 2 |
∴x+|PQ|的最小值是|QF|-1=3-1=2，
故选：A．
点评：本题考查抛物线的简单性质，考查抛物线的定义，比较基础．
练习册系列答案
相关题目
在（
+1）10的展开式中，x4的项的系数是（ ）
| x |
| A、45 | B、50 | C、55 | D、60 |
已知函数f（x）=x3-x2+1，则f（x）在点（1，1）处的切线的倾斜角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|-1＜x＜1}，B={x|x（x-2）＜0}，则A∩B（ ）
| A、{x|-1＜x＜0} |
| B、{x|0＜x＜1} |
| C、{x|-1＜x＜2} |
| D、{x|x＞2} |
平面α的一个法向量为（1，2，0），平面β的一个法向量为（2，-1，0），则平面α与平面β的位置关系是（ ）
| A、平行 | B、相交但不垂直 |
| C、垂直 | D、不能确定 |
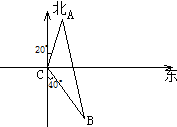如图，已知两座灯塔A和B与海洋观察站C的距离都等于1km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为（ ）| A、1km | ||
B、
| ||
C、
| ||
| D、2km |
“所有9的倍数都是3的倍数．某数是9的倍数，故该数为3的倍数，”上述推理（ ）
| A、完全正确 |
| B、推理形式不正确 |
| C、错误，因为大小前提不一致 |
| D、错误，因为大前提错误 |
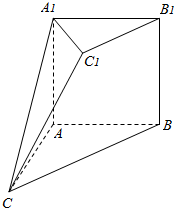如图，在多面体ABC-A1B1C1中，四边形A1ABB1是边长为a的正方形，AB=AC，BC=