题目内容
已知函数f(x)=x2-ax+1-a在区间(0,1)上有两个零点,则实数a的取值范围为 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由题意,只要f(0)>0,f(1)>0并且对称轴在(0,1)之间,f(
)<0,解不等式组即可.
| a |
| 2 |
解答:
解:由题意,要使函数f(x)=x2-ax+1-a在区间(0,1)上有两个零点,
只要
,解得2
-2<a<1,
所以实数a的取值范围为(2
-2,1);
故答案为:(2
-2,1)
只要
|
| 2 |
所以实数a的取值范围为(2
| 2 |
故答案为:(2
| 2 |
点评:本题考查了函数零点的分布,关键是结合二次函数图象等价得到不等式组.

练习册系列答案
相关题目
 已知一个圆锥的地面半径为R,高为
已知一个圆锥的地面半径为R,高为 已知函数f(x)=ax2+(a-1)x+b的最小值为-1,且f(0)=-1.
已知函数f(x)=ax2+(a-1)x+b的最小值为-1,且f(0)=-1. 在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )
在空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,0),(1,0,1),(1,1,0),(0,1,1),且该四面体的俯视图如图,则左视图为( )
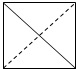
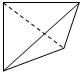
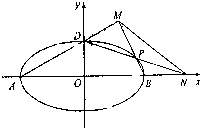 已知椭圆
已知椭圆