题目内容
 已知一个圆锥的地面半径为R,高为
已知一个圆锥的地面半径为R,高为| 15 |
(1)若该圆锥中有一个内接正方体,求该正方体的棱长;
(2)有一只虫子从P点绕着圆锥面爬行到M点(如图中曲线PM),求该虫爬过的最短距离.
考点:多面体和旋转体表面上的最短距离问题
专题:计算题,空间位置关系与距离
分析:(1)设该正方体的棱长为a,则利用轴截面可得
=
,即可求出该正方体的棱长;
(2)求出VP=4R,圆锥的侧面展开图为扇形,弧长为2πR,圆心角为
,即可求出该虫爬过的最短距离
| ||||
| R |
| ||
|
(2)求出VP=4R,圆锥的侧面展开图为扇形,弧长为2πR,圆心角为
| π |
| 2 |
解答:
解:(1)设该正方体的棱长为a,则利用轴截面可得
=
,
∴a=
R;
(2)一个圆锥的底面半径为R,高为
R,∴VP=4R,
圆锥的侧面展开图为扇形,弧长为2πR,圆心角为
,
∴该虫爬过的最短距离为
=2
R.
| ||||
| R |
| ||
|
∴a=
15
| ||||
| 13 |
(2)一个圆锥的底面半径为R,高为
| 15 |
圆锥的侧面展开图为扇形,弧长为2πR,圆心角为
| π |
| 2 |
∴该虫爬过的最短距离为
| 4R2+16R2 |
| 5 |
点评:本题考查多面体和旋转体表面上的最短距离问题,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
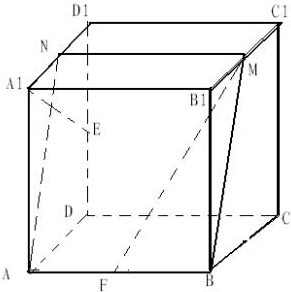 如图,在正方体ABCD-A1B1C1D1中,M,N,E,F,F分别是棱B1C1,A1D1,D1D,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N,E,F,F分别是棱B1C1,A1D1,D1D,AB的中点.