题目内容
13.在直角坐标系xOy中,直线l过点M(3,4),其倾斜角为45°,圆C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}\right.(θ为参数)$.再以原点为极点,以x正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy有相同的长度单位.(1)求圆C的极坐标方程;
(2)设圆C与直线l交于点A、B,求|MA|•|MB|的值.
分析 (1)利用cos2θ+sin2θ=1消去参数可得圆的直角坐标方程式,由极坐标与直角坐标互化公式代入化简即可得出.
(2)直线l的参数方程$\left\{\begin{array}{l}{x=3+tcos4{5}^{°}}\\{y=4+tsin4{5}^{°}}\end{array}\right.$,(t为参数),代入圆方程得:${t}^{2}+5\sqrt{2}t$+9=0,利用|MA|•|MB|=|t1|•|t2|=|t1t2|即可得出.
解答 解:(1)消去参数可得圆的直角坐标方程式为x2+(y-2)2=4,
由极坐标与直角坐标互化公式得(ρcosθ)2+(ρsinθ-2)2=4化简得ρ=4sinθ,
(2)直线l的参数方程$\left\{\begin{array}{l}{x=3+tcos4{5}^{°}}\\{y=4+tsin4{5}^{°}}\end{array}\right.$,(t为参数).
即$\left\{\begin{array}{l}x=3+\frac{{\sqrt{2}}}{2}t\\ y=4+\frac{{\sqrt{2}}}{2}t\end{array}\right.(t为参数)$代入圆方程得:${t}^{2}+5\sqrt{2}t$+9=0,
设A、B对应的参数分别为t1、t2,则${t_1}+{t_2}=5\sqrt{2}$,t1t2=9,
于是|MA|•|MB|=|t1|•|t2|=|t1t2|=9.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、直线参数方程的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.设经过椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上的任意两点的连线(该连线不与x轴垂直)的垂直平分线与x轴交点的横坐标为x0,则x0的取值范围是( )
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-1,1] | D. | (-1,1) |
1.如图是一个四棱锥的三视图,则该几何体的体积为( )


| A. | 16 | B. | 12 | C. | 9 | D. | 8 |
18.在一次跳高比赛前,甲、乙两名运动员各试跳了一次.设命题p表示“甲的试跳成绩超过2米”,命题q表示“乙的试跳成绩超过2米”,则命题p∨q表示( )
| A. | 甲、乙恰有一人的试跳成绩没有超过2米 | |
| B. | 甲、乙至少有一人的试跳成绩没有超过2米 | |
| C. | 甲、乙两人的试跳成绩都没有超过2米 | |
| D. | 甲、乙至少有一人的试跳成绩超过2米 |
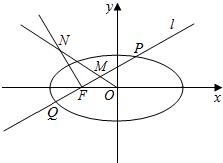 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{2}$),离心率为$\frac{\sqrt{6}}{3}$,点O为坐标原点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{2}$),离心率为$\frac{\sqrt{6}}{3}$,点O为坐标原点.