题目内容
18.已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E,F分别是AB,AD的中点,则点C到平面GEF的距离为$\frac{6\sqrt{11}}{11}$.分析 设点C到平面GEF的距离为h,由题意利用等体积法可得 VC-GEF=VG-CEF,由此求得h的值.
解答 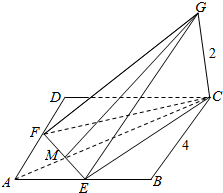 解:设点C到平面GEF的距离为h,由题意可得CE=CF=$\sqrt{{BC}^{2}{+BE}^{2}}$=2$\sqrt{5}$,
解:设点C到平面GEF的距离为h,由题意可得CE=CF=$\sqrt{{BC}^{2}{+BE}^{2}}$=2$\sqrt{5}$,
∴GE=GF=$\sqrt{{CG}^{2}{+CE}^{2}}$=$\sqrt{{2}^{2}+{(2}^{2}{+4}^{2})}$=2$\sqrt{6}$.
取EF的中点为M,则CM=$\frac{3}{4}$AC=$\frac{3}{4}$•4$\sqrt{2}$=3$\sqrt{2}$,∴GM=$\sqrt{{CG}^{2}{+CM}^{2}}$=$\sqrt{{2}^{2}+(3\sqrt{2})^{2}}$=$\sqrt{4+18}$=$\sqrt{22}$.
∵VC-GEF=VG-CEF,∴$\frac{1}{3}$•($\frac{1}{2}$•EF•GM)•h=$\frac{1}{3}$•($\frac{1}{2}$•EF•CM)•CG,
即 GM•h=CM•CG,即 $\sqrt{22}$•h=3$\sqrt{2}$•2,求得 h=$\frac{6\sqrt{11}}{11}$,
即点C到平面GEF的距离为$\frac{6\sqrt{11}}{11}$,
故答案为:$\frac{6\sqrt{11}}{11}$.
点评 本题主要考查空间距离的求法,用等体积法求点到平面的距离,属于中档题.

练习册系列答案
相关题目
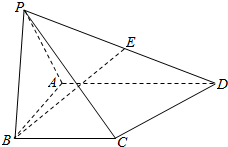 如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.
如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.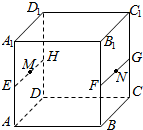 若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )
若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )