题目内容
12.以下表示x轴的参数方程是( )| A. | $\left\{\begin{array}{l}{x={t}^{2}+1}\\{y=0}\end{array}\right.$(t为参数) | B. | $\left\{\begin{array}{l}{x=0}\\{y=3t+1}\end{array}\right.$(t为参数) | ||
| C. | $\left\{\begin{array}{l}{x=1+sinθ}\\{y=0}\end{array}\right.$(θ为参数) | D. | $\left\{\begin{array}{l}{x=4t+1}\\{y=0}\end{array}\right.$(t为参数) |
分析 根据x轴上点的坐标特点判断.
解答 解:由于x轴上的点纵坐标为0,排除B,
由于x轴上的点横坐标可以是任意实数,故排除A,C.
故选D.
点评 本题考查了直线的参数方程,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设经过椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上的任意两点的连线(该连线不与x轴垂直)的垂直平分线与x轴交点的横坐标为x0,则x0的取值范围是( )
| A. | (-$\frac{1}{2}$,$\frac{1}{2}$) | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-1,1] | D. | (-1,1) |
1.如图是一个四棱锥的三视图,则该几何体的体积为( )


| A. | 16 | B. | 12 | C. | 9 | D. | 8 |
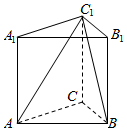 如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.
如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.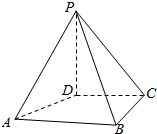 如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.