题目内容
已知数列{an}的前n项和为Sn,且Sn=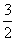 an-1(n∈N*).
an-1(n∈N*).
(1)求数列{an}的通项公式;
(2)在数列{bn}中,b1=5,bn+1=bn+an,求数列{bn}的通项公式.
(1)当n=1时,S1=a1=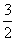 a1-1,所以a1=2.
a1-1,所以a1=2.
∵Sn=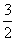 an-1,①
an-1,①
∴当n≥2时,Sn-1=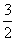 an-1-1,②
an-1-1,②
①-②,得an=(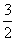 an-1)-(
an-1)-(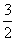 an-1-1),
an-1-1),
所以an=3an-1,又a1≠0,故an-1≠0,
所以 =3,
=3,
故数列{an}是首项为2,公比为3的等比数列,
所以an=2·3n-1.
(2)由(1)知bn+1=bn+2·3n-1.
当n≥2时,bn=bn-1+2·3n-2,
…
b3=b2+2·31,
b2=b1+2·30,
将以上n-1个式子相加并整理,得bn=b1+2×(3n-2+…+31+30)=5+2×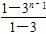 =3n-1+4.
=3n-1+4.
当n=1时,31-1+4=5=b1,
所以bn=3n-1+4(n∈N*).

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如表定义函数f(x):
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 5 | 4 | 3 | 1 | 2 |
对于数列{an},a1=4,an=f(an-1),n=2,3,4,…,则a2014的值是( )
A.1 B.2 C.3 D.4
 =-2,则|
=-2,则| |的最小值是________.
|的最小值是________.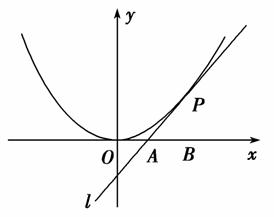
 =0,求点M的轨迹C;
=0,求点M的轨迹C;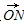 =a15
=a15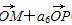 (直线MP不过点O),则S20等于( )
(直线MP不过点O),则S20等于( ) B.5 C.-
B.5 C.-