题目内容
13.在△ABC中,a,b,c分别是角A,B,C的对边,若2sin2A=3cosA,b2+c2-a2+mbc=0,则实数m的值为( )| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
分析 利用同角三角函数的平方关系,化简方程,即可求∠A的大小,利用余弦定理,结合bc≠0,即可求m的值.
解答 解:∵3cosA-2sin2A=0,
∴3cosA-2+2cos2A=0,
∴(cosA+2)(2cosA-1)=0,
∴cosA=$\frac{1}{2}$
∵A∈(0,π),
∴∠A=$\frac{π}{3}$,
∵b2+c2-a2+mbc=0,
∴由余弦定理可得:2bccosA+mbc=0,即:bc+mbc=bc(1+m)=0,
∴由bc≠0,解得:m=-1.
故选:C.
点评 本题考查同角三角函数的平方关系,考查余弦定理的运用,考查学生的计算能力,属于基础题.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
4.下列函数中,是偶函数的是( )
| A. | y=2x | B. | y=x2 | C. | y=2x | D. | y=log2x |
18.(题类B)设f(x)=sinx2,则f′(x)等于( )
| A. | sin2x | B. | cosx2 | C. | 2xsinx2 | D. | 2xcosx2 |
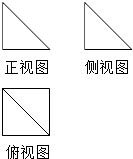 一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.
一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.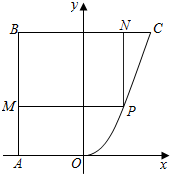 某地有如图所示的一块不规则的非农业用地ABCO,且AB⊥BC,OA∥BC,AB=BC=4km,AO=2km,曲线段OC是以O为顶点,开口向上,且对称轴平行于AB的抛物线的一段.当地政府为科技兴市,欲将该地规划建成一个矩形高科技工业园区PMBN,矩形的相邻两边BM,BN分别落在AB,BC上,顶点P在曲线段OC上.问应如何规划才能使矩形园区的用地面积最大?并求出最大的用地面积(精确到0.1 km2).
某地有如图所示的一块不规则的非农业用地ABCO,且AB⊥BC,OA∥BC,AB=BC=4km,AO=2km,曲线段OC是以O为顶点,开口向上,且对称轴平行于AB的抛物线的一段.当地政府为科技兴市,欲将该地规划建成一个矩形高科技工业园区PMBN,矩形的相邻两边BM,BN分别落在AB,BC上,顶点P在曲线段OC上.问应如何规划才能使矩形园区的用地面积最大?并求出最大的用地面积(精确到0.1 km2).