题目内容

直线x-y+2=0与曲线（x-1）（x-2）+（y-3）（y-4）=0的交点个数是
 
．
考点：直线的一般式方程
专题：直线与圆
分析：联立
x-y+2=0
(x-1)(x-2)+(y-3)(y-4)=0
解得即可．
解答： 解：联立
x-y+2=0
(x-1)(x-2)+(y-3)(y-4)=0
解得
x=1
y=3
，
x=2
y=4
．
∴交点为（1，3），（2，4）．
因此直线x-y+2=0与曲线（x-1）（x-2）+（y-3）（y-4）=0的交点个数是2．
故答案为：2．
点评：本题考查了直线与圆的位置关系及交点个数，属于基础题．
练习册系列答案
相关题目
（1）已知A（-3，4），B（2，
3
），在x轴上找一点P，使|PA|=|PB|，并求|PA|的值；
（2）已知点M（x，-4）与N（2，3）间的距离为7
2
，求x的值．
已知直线l1的倾斜角为30°，直线l1⊥l2，则直线l2的斜率是
 
．
已知p：x 2-2x-3＜0，q：
1
x-2
＜0，若p且q为真，则x的取值范围是
 
．
已知sin
θ
2
+cos
θ
2
=
5
2
那么sinθ的值为
 
，cos2θ的值为
 
．
集合A={y|y=-x2+4，x=-1，0，1，2}，B={y|y≥1}，则A∩B=
 
．
已知数列{an}满足：
1
an+1
-
1
an
=1，且a1=1，则an=
 
．
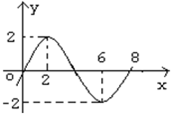函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+…+f（11）的值是（　　）
A、2+2
2
B、2-2
2
C、0
D、-1
方程sinx=-cos80°的解集是（　　）
A、{X|X=k•180°+10°，k∈z}
B、{x|x=k•360°+10°，k∈z}
C、{x|x=k•180°±10°，k∈z}
D、{x|x=k•180°-（-1）k•10°，k∈z}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网