题目内容
10.有下列五个命题:(1)在平面内,F1、F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则点M的轨迹是椭圆;
(2)过M(2,0)的直线L与椭圆$\frac{{x}^{2}}{2}$+y2=1交于P1、P2两点,线段P1P2中点为P,设直线L的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于-$\frac{1}{2}$;
(3)“若-3<m<5,则方程$\frac{x^2}{5-m}+\frac{y^2}{m+3}=1$是椭圆”;
(4)椭圆$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{6}$=1的两个焦点为F1,F2,点P为椭圆上的点,则能使$∠{F_1}P{F_2}=\frac{π}{2}$的点P的个数0个;
(5)“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的必要不充分条件;
其中真命题的序号是(2)、(4).
分析 (1)在平面内,F1、F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则点M的轨迹是线段F1F2,即可判断出正误;
(2)设P1(x1,y1),P2(x2,y2),线段P1P2中点P(x0,y0),代入椭圆方程可得:$\frac{({x}_{2}+{x}_{1})({x}_{2}-{x}_{1})}{2}$+(y2+y1)(y2-y1)=0,化为1+2k1k2=0,即可判断出正误;(3)方程$\frac{x^2}{5-m}+\frac{y^2}{m+3}=1$是椭圆?$\left\{\begin{array}{l}{5-m>0}\\{m+3>0}\\{5-m≠m+3}\end{array}\right.$,解得m范围即可判断出正误;
(4)椭圆$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{6}$=1的两个焦点为F1,F2,点P为椭圆上的点,取椭圆的短轴端点P(0,$\sqrt{6}$),则∠F1PF2为最大角,而tan∠F1PO=$\frac{c}{b}$=$\frac{2}{\sqrt{6}}$<1,即可判断出正误;
(5)由直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0,对m分类讨论:利用两条直线垂直的充要条件即可得出正误.
解答 解:(1)在平面内,F1、F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则点M的轨迹是线段F1F2,不是椭圆,是假命题;
(2)设P1(x1,y1),P2(x2,y2),线段P1P2中点P(x0,y0),由于$\frac{{x}_{1}^{2}}{2}+{y}_{1}^{2}$=1,$\frac{{x}_{2}^{2}}{2}$+${y}_{2}^{2}$=1,相减可得:$\frac{({x}_{2}+{x}_{1})({x}_{2}-{x}_{1})}{2}$+(y2+y1)(y2-y1)=0,化为x0+k1•2y0=0,∴1+2k1k2=0,因此k1k2等于-$\frac{1}{2}$,是真命题;
(3)方程$\frac{x^2}{5-m}+\frac{y^2}{m+3}=1$是椭圆?$\left\{\begin{array}{l}{5-m>0}\\{m+3>0}\\{5-m≠m+3}\end{array}\right.$,解得-3<m<5,m≠1,因此“若-3<m<5,则方程$\frac{x^2}{5-m}+\frac{y^2}{m+3}=1$是椭圆”是假命题;
(4)椭圆$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{6}$=1的两个焦点为F1,F2,点P为椭圆上的点,取椭圆的短轴端点P(0,$\sqrt{6}$),则∠F1PF2为最大角,而tan∠F1PO=$\frac{c}{b}$=$\frac{2}{\sqrt{6}}$<1,∴$0<∠{F}_{1}PO<\frac{π}{4}$,∴0<∠F1PF2<$\frac{π}{2}$,因此能使$∠{F_1}P{F_2}=\frac{π}{2}$的点P的个数0个,是真命题;
(5)由直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0,对m分类讨论:当m=0时,两条直线分别化为:2x+1=0,-2x+2y-3=0,此时两条直线不垂直,舍去;当m=-2时,两条直线分别化为:-2y+1=0,-4x-3=0,此时两条直线垂直,因此m=-2;当m≠0,-2时,由于两条直线垂直可得:-$\frac{m+2}{m}$×$\frac{2-m}{m+2}$=-1,解得m=1.综上可得:此两条直线垂直的充要条件为:m=-2或1,因此“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充分不必要条件.是假命题.
综上可得:真命题为(2)、(4).
答案为:(2)、(4).
点评 本题考查了简易逻辑的判定方法、圆锥曲线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案| A. | $[{-1,\frac{1}{2}}]$ | B. | $[{-2,\frac{1}{2}}]$ | C. | [-1,0] | D. | [-2,0] |
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
 《算法统宗》是中国古代数学名著,由明代数学家程大位编著.《算法统宗》对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“竹筒容米”就是其中一首:家有九節竹一莖,為因盛米不均平;下頭三節三升九,上梢四節貯三升;唯有中間二節竹,要將米數次第盛;若是先生能算法,也教算得到天明!大意是:用一根9节长的竹子盛米,每节竹筒盛米的容积是不均匀的.下端3节可盛米3.9升,上端4节可盛米3升.要按依次盛米容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出中间两节的容积为( )
《算法统宗》是中国古代数学名著,由明代数学家程大位编著.《算法统宗》对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“竹筒容米”就是其中一首:家有九節竹一莖,為因盛米不均平;下頭三節三升九,上梢四節貯三升;唯有中間二節竹,要將米數次第盛;若是先生能算法,也教算得到天明!大意是:用一根9节长的竹子盛米,每节竹筒盛米的容积是不均匀的.下端3节可盛米3.9升,上端4节可盛米3升.要按依次盛米容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出中间两节的容积为( )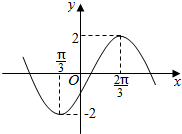 已知函数f(x)=Asin(ωx+φ)(其中A,ω,φ为常数,且A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示:
已知函数f(x)=Asin(ωx+φ)(其中A,ω,φ为常数,且A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示: 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,过EF的截面EFG与底面成60°二面角,且与棱AA1交于G,求棱锥G-AEF的体积.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,过EF的截面EFG与底面成60°二面角,且与棱AA1交于G,求棱锥G-AEF的体积.