题目内容
对集合A={1,2},B={1,2,3}及平面上的点M(a,b)(a∈A,b∈B),记“点M(a,b)落在直线x+y=3或x+y=4上”为事件P,则事件P发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:由题意可得总的基本事件共6个,其中事件P包含其中5个,由古典概型的概率公式可得.
解答:
解:∵集合A={1,2},B={1,2,3},
∴分别从集合A和B中随机取一个数a和b,确定的点M(a,b)共有2×3=6个,
而满足“点M(a,b)落在直线x+y=3或x+y=4上”的事件P
有(1,2)、(2,1),(1,3),(2,2)共4个,
∴事件P发生的概率为
=
故选:C
∴分别从集合A和B中随机取一个数a和b,确定的点M(a,b)共有2×3=6个,
而满足“点M(a,b)落在直线x+y=3或x+y=4上”的事件P
有(1,2)、(2,1),(1,3),(2,2)共4个,
∴事件P发生的概率为
| 4 |
| 6 |
| 2 |
| 3 |
故选:C
点评:本题考查古典概型及概率公式,属基础题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,已知
=(-1,t),
=(1,1),若∠ABO=90°,则实数t的值为( )
| OA |
| OB |
| A、3 | B、1 | C、0 | D、-1 |
直线y=kx+b与圆(x-1)2+(y-2)2=5有公共点的一个充分不必要条件为( )
| A、b≤4 | B、b≥0 |
| C、-4≤b≤4 | D、0≤b≤4 |
已知三角形的三条边成公差为2的等差数列,且它的最大角的正弦值为
,则这个三角形的面积是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数y=sin(2x+
)的图象向左平移
个单位,再向上平移2个单位,则所得函数的表达式是( )
| π |
| 4 |
| π |
| 4 |
A、y=sin(2x-
| ||
B、y=cos(2x+
| ||
C、y=sin(2x+
| ||
D、y=cos(2x-
|
若b为a,c的等比中项,则函数y=ax2+bx+c的零点个数是( )
| A、0 | B、1 |
| C、2 | D、A、B、C都有可能 |
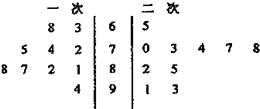 如图是某同学一学期两次考试成绩的茎叶图,现从该同学两次考试成绩中各取一科成绩,则这两科成绩都在80分以上的概率为( )
如图是某同学一学期两次考试成绩的茎叶图,现从该同学两次考试成绩中各取一科成绩,则这两科成绩都在80分以上的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|