题目内容
复数z=（3m-2）+（m-1）i，m∈R．
（1）m为何值时，z是纯虚数？
（2）m取什么值时，z在复平面内对应的点位于第四象限？
（1）m为何值时，z是纯虚数？
（2）m取什么值时，z在复平面内对应的点位于第四象限？
考点：复数的基本概念,复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：（1）通过复数的实部为0，虚部不为0求出m值，z是纯虚数．
（2）z在复平面内对应的点位于第四象限，列出关系式，求出m值．
（2）z在复平面内对应的点位于第四象限，列出关系式，求出m值．
解答：
解：（1）复数z=（3m-2）+（m-1）i，m∈R．z是纯虚数，
∴
，解得m=
，此时复数是纯虚数．
（2）z在复平面内对应的点位于第四象限，
∴
，解得
＜m＜1，此时复数对应的点位于第四象限．
∴
|
| 2 |
| 3 |
（2）z在复平面内对应的点位于第四象限，
∴
|
| 2 |
| 3 |
点评：本题考查复数的基本概念的应用，是基础题．
练习册系列答案
相关题目
设双曲线
-
=1（a＞0，b＞0）的离心率为
，且它的一个焦点在抛物线y2=12x的准线上，则此双曲线的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在半径为4，圆心角为变量2θ（0＜θ＜2π）的扇形OAB内作一内切圆P，再在扇形内作一个与扇形两半径相内切并与圆P外切的小圆Q，记圆Q的半径为y．
如图，三棱锥P-ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=4，E为PC的中点，M为AB的中点，点F在PA上，且AF=2FP．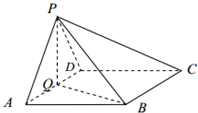
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．