题目内容
四边形ABCD内接于椭圆
+
=1,其中A的横坐标为4,C的纵坐标为5,求四边形ABCD面积的最大值.
| x2 |
| 16 |
| y2 |
| 25 |
考点:椭圆的简单性质
专题:数形结合法,圆锥曲线的定义、性质与方程
分析:根据题意,画出图形,结合图形得出椭圆的内接四边形ABCD面积取最大值时,对角线BD过AC的中点M和原点O;
求出B、D点的坐标,从而求出点B、D到AC的距离,即可求出四边形ABCD的最大面积.
求出B、D点的坐标,从而求出点B、D到AC的距离,即可求出四边形ABCD的最大面积.
解答:
解:根据题意,画出图形,如图所示 ;
;
∵椭圆
+
=1,
∴A(4,0),C(0,5);
由图形知,椭圆的内接四边形ABCD面积取最大值时,对角线BD过AC的中点M和原点O;
∵直线AC的方程是
+
=1,
点M(2,
),
∴直线BD的方程是y=
x;
∴
,
解得
,
;
∴点B(2
,
)到直线AC的距离是d1=
=
;
同理,点D(-2
,
)到直线AC的距离是d2=
;
∴四边形ABCD的最大面积为
S=S△ABC+S△ADC=
×|AC|d1+
×|AC|d2=
×
×(
+
)=20
.
 ;
;∵椭圆
| x2 |
| 16 |
| y2 |
| 25 |
∴A(4,0),C(0,5);
由图形知,椭圆的内接四边形ABCD面积取最大值时,对角线BD过AC的中点M和原点O;
∵直线AC的方程是
| x |
| 4 |
| y |
| 5 |
点M(2,
| 5 |
| 2 |
∴直线BD的方程是y=
| 5 |
| 4 |
∴
|
解得
|
|
∴点B(2
| 2 |
5
| ||
| 2 |
|
| ||||||||||
|
20(
| ||
|
同理,点D(-2
| 2 |
5
| ||
| 2 |
20(
| ||
|
∴四边形ABCD的最大面积为
S=S△ABC+S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 42+52 |
20(
| ||
|
20(
| ||
|
| 2 |
点评:本题考查了直线与圆锥曲线的应用问题,解题时应利用数形结合法,分析解题思路,从而写出解题过程,是综合性题目.

练习册系列答案
相关题目
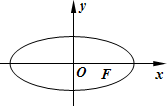 已知椭圆
已知椭圆