题目内容
16.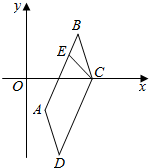 如图,在平行四边形ABCD中,边AB所在的直线方程为2x-y-2=0,点C(2,0),D(1,t),t∈R.
如图,在平行四边形ABCD中,边AB所在的直线方程为2x-y-2=0,点C(2,0),D(1,t),t∈R.(1)求AB边上的高CE所在的直线方程;
(2)求平行四边形ABCD的面积.
分析 (1)根据垂直得出kCE=-$\frac{1}{2}$,再由经过点C,即可求出方程.
(2)利用点到直线的距离公式求出|CE|,再根据点点之间的距离公式求出|CD|,即可求出面积
解答 解:(1)∵边AB所在直线方程为2x-y-2=0
∴kCE=-$\frac{1}{2}$
又∵CE经过点C(2,0)
∴AB边上的高CE所在直线的方程为:y=-$\frac{1}{2}$x+1;
(2)点C到直线AB:2x-y-2=0的距离|CE|=$\frac{|4-0-2|}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∵C(2,0),D(1,t),
∴kCD=$\frac{t}{1-2}$=-t,
∵AB∥CD,
∴kCD=kAB=2,
∴t=-2,
∴|CD|=$\sqrt{(1-2)^{2}+(-2-0)^{2}}$=$\sqrt{5}$,
∴S=|CD|•|CE|=$\sqrt{5}$•$\frac{2\sqrt{5}}{5}$=2.
点评 此题考查了两直线平行、垂直的条件以及点到直线的距离公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目