题目内容
12.函数y=${2}^{\sqrt{{x}^{2}-1}}$的定义域为(-∞,-1]∪[1,+∞),值域为[1,+∞).分析 由题意可得x2-1≥0,从而确定定义域,由观察法求函数的值域.
解答 解:∵x2-1≥0,
∴x≥1或x≤-1,
∵$\sqrt{{x}^{2}-1}$≥0,
∴y=${2}^{\sqrt{{x}^{2}-1}}$≥1,
∴函数y=${2}^{\sqrt{{x}^{2}-1}}$的定义域为(-∞,-1]∪[1,+∞),
值域为[1,+∞).
故答案为:(-∞,-1]∪[1,+∞),[1,+∞).
点评 本题考查了函数的定义域与值域的求法的应用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
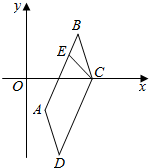 如图,在平行四边形ABCD中,边AB所在的直线方程为2x-y-2=0,点C(2,0),D(1,t),t∈R.
如图,在平行四边形ABCD中,边AB所在的直线方程为2x-y-2=0,点C(2,0),D(1,t),t∈R.