题目内容

8．设等差数列{an}中的a1=1，且a3+a5=14，求数列{an}的通项公式和前10项的和S10．

分析 利用等差数列的通项公式先求出公差d，由此能求出数列{an}的通项公式和前10项的和S10．

解答 解：∵等差数列{an}中的a1=1，且a3+a5=14，
∴1+2d+1+4d=14，解得d=2，
∴数列{an}的通项公式和前10项的和：
S10=10×1+$\frac{10×9}{2}×2$=100．

点评 本题考查数列前10项和的求法，是基础题，解题时要认真审题，注意等差数列的通项公式和前n项和公式的合理运用．

练习册系列答案
相关题目
19．计算：（$\frac{27}{8}$）${\;}^{-\frac{1}{3}}$+log2（log216）=$\frac{8}{3}$．
20．在?ABCD中，若A（-2，0），B（6，8），C（8，0），求D点的坐标．
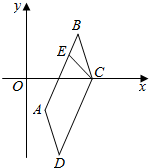16．如图，在平行四边形ABCD中，边AB所在的直线方程为2x-y-2=0，点C（2，0），D（1，t），t∈R．
（1）求AB边上的高CE所在的直线方程；
（2）求平行四边形ABCD的面积．
3．将下列各数：40.9，80.48，（$\frac{1}{2}$）-1.5按从小到大排序为40.9＞（$\frac{1}{2}$）-1.5＞80.48．
13．己知抛物线y2=2px（p＞0）上两个动点A（x1，y1），B（x2，y2），O为坐标原点，OA⊥OB．
（1）求线段AB中点的轨迹方程；
（2）若在C上的点到直线x-2y+2$\sqrt{5}$-p=0的距离为d，求d的最小值．
20．已知直线l1经过点A（0，-1）和点B（-$\frac{4}{a}$，1），直线l2经过点M（1，1）和点N（0，-2），若l1与l2没有公共点，则实数a的值为-6．
17．（1）化简$\sqrt{1-si{n}^{2}100°}$；
（2）用tanα表示$\frac{sinα+cosα}{2sinα-cosα}$，sin2α+sinαcosα+3cos2α
15．已知集合A={x|x＜2}，B={x|-1≤x≤3}，则A∩B=（　　）
A．[-1，2）B．[-1，3]C．（-∞，3]D．[-1，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网