题目内容
20.已知集合A={0,1,2},全集U={x-y|x∈A,y∈A},则∁UA={-2,-1}.分析 先求出集合U,由此能求出∁UA.
解答 解:∵A={0,1,2},全集U={x-y|x∈A,y∈A},
∴全集U={-2,-1,0,1,2}
∁UA={-2.-1}.
故答案为:{-2,-1}.
点评 本题考查补集的求法,是基础题,解题时要认真审题,注意补集性质的合理运用.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
8.方程ex=2-x的根位于( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
5.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线与直线x=$\frac{{a}^{2}}{c}$分别交于A,B两点,F为该双曲线的右焦点,若90°<∠AFB<120°,则该双曲线离心率的取值范围是( )
| A. | (1,$\sqrt{2}$) | B. | ($\frac{2\sqrt{3}}{3}$,+∞) | C. | (1,$\frac{2\sqrt{3}}{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线y2=12x的焦点重合,且双曲线的离心率等于$\sqrt{3}$,则该双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
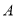 如果满足:①
如果满足:① ;②若对
;②若对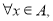 有
有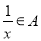 ,则称
,则称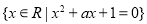 ;
;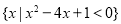 ;
; .其中“互倒集”的个数是( )
.其中“互倒集”的个数是( )