题目内容
已知复数z满足z-|z|=-1+i(i是虚数单位),则z= .
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则和模的计算公式即可得出.
解答:
解:设z=a+bi,(a,b∈R).
∵复数z满足z-|z|=-1+i,
∴a+bi-
=-1+i,
∴
,解得
.
∴z=i.
故答案为:i.
∵复数z满足z-|z|=-1+i,
∴a+bi-
| a2+b2 |
∴
|
|
∴z=i.
故答案为:i.
点评:本题考查了复数的运算法则和模的计算公式,属于基础题.

练习册系列答案
相关题目
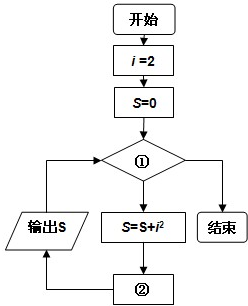 如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )
如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )| A、i≤2014,i=i+1 |
| B、i≤1007,i=i+1 |
| C、i≤2014,i=i+2 |
| D、i≤1007,i=i+2 |
设集合U={1,2,3,4},A={1,2,4},B={2,3,4},则∁U(A∩B)等于( )
| A、{1,2} |
| B、{1,4} |
| C、{1,3} |
| D、{2,4} |
在长为20cm的线段AB上任取一点P,并且以线段AP为边作正三角形,则这个正三角形的面积介于
cm2与16
cm2之间的概率为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
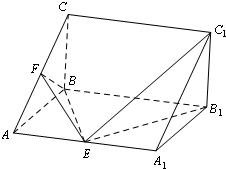 如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=
如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=