题目内容
20.在平面直角坐标系中,动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,记点P的轨迹为曲线W,则下列命题中:①曲线W关于原点对称;
②曲线W关于x轴对称;
③曲线W关于y轴对称;
④曲线W关于直线y=x对称
所有真命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据距离相等列出方程化简求出y关于x的函数,作出图象即可得出结论.
解答  解:曲线W的轨迹方程为|x|+|y|=$\sqrt{(x-1)^{2}+(y-1)^{2}}$,
解:曲线W的轨迹方程为|x|+|y|=$\sqrt{(x-1)^{2}+(y-1)^{2}}$,
两边平方得:2|xy|=-2x-2y+2,
即|xy|+x+y=1,
①若xy>0,则xy+x+y+1=2,即(x+1)(y+1)=2,
∴y=$\frac{2}{x+1}-1$,函数为以(-1,-1)为中心的双曲线的一支,
②若xy<0,则xy-x-y+1=0,即(x-1)(y-1)=0,
∴x=1(y<0)或y=1(x<0).
作出图象如图所示:
∴曲线W关于直线y=x对称;
故选A.
点评 本题考查了轨迹方程的求解,函数图象的对称性,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
11.数字0,1,2,3,4可以组成( )个无重复数字的五位数.
| A. | 96 | B. | 120 | C. | 625 | D. | 1024 |
8.用一个“+”号和一个“-”号将数字 1,2,3连成算式,不同的运算结果共有( )
| A. | 12种 | B. | 6种 | C. | 4种 | D. | 3种 |
5.已知复数z=a2+(b-2)i的实部和虚部分别是2和3,则实数a,b的值分别是( )
| A. | $\sqrt{2}$,1 | B. | $\sqrt{2}$,5 | C. | ±$\sqrt{2}$,5 | D. | ±$\sqrt{2}$,1 |
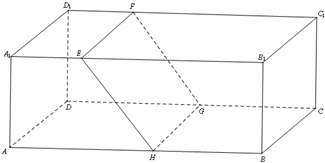 如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.
如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.