题目内容
从甲地到乙地途经丙地，其中甲、乙两地相距200千米，甲、丙两地相距离80千米，某人开汽车以40千米/小时的速度从甲地到达乙地，在丙地停留1小时，把汽车离开甲地的路程s表示为时间t（小时）的函数表达式是 ．
考点：根据实际问题选择函数类型
专题：应用题,函数的性质及应用
分析：由题意，从甲到乙需要2小时，从乙到丙需要3小时，在丙地停留1小时，所以我们用分段函数表示函数的解析式．
解答：
解：由题意，从甲到乙需要2小时，从乙到丙需要3小时，
∴当0≤t≤2时，s=40t；
在丙地停留1小时，即2＜t≤3，s=80；
当3＜t≤6时，s=40（t-1）；
∴汽车离开甲地的路程s表示为时间t（小时）的函数表达式是s=
，
故答案为s=
．
∴当0≤t≤2时，s=40t；
在丙地停留1小时，即2＜t≤3，s=80；
当3＜t≤6时，s=40（t-1）；
∴汽车离开甲地的路程s表示为时间t（小时）的函数表达式是s=
|
故答案为s=
|
点评：由于在不同的时间，汽车离开甲地的路程有所不同，所以函数的解析式是分段的，要注意变量范围的确定．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
下列函数中既是偶函数又在（0，+∞）上是增函数的是（ ）
| A、y=x3 | ||
| B、y=|x|+1 | ||
C、f（x）=
| ||
| D、y=20 -|x| |
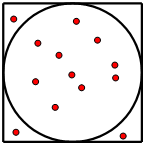某同学动手做实验：《用随机模拟的方法估计圆周率的值》，在左下图的正方形中随机撒豆子，每个豆子落在正方形内任何一点是等可能的，若他随机地撒50粒统计得到落在圆内的豆子数为35粒，则由此估计出的圆周率π的值为按照如图的程序图计算，若开始输入的值为3，则最后输出的结果是（ ）
| A、6 | B、21 |
| C、5050 | D、231 |