题目内容
下列函数中既是偶函数又在(0,+∞)上是增函数的是( )
| A、y=x3 | ||
| B、y=|x|+1 | ||
C、f(x)=
| ||
| D、y=20 -|x| |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:利用奇偶函数的判断方法,对四个选项①分别明确定义域;②如果个于原点对称,再判断f(-x)与f(x)的关系.
解答:
解:对于选项A,定义域为R,但是(-x)3=-x3,是奇函数;
对于B,定义域为R,并且|-x|+1=|x|+1,是偶函数,并且在(0,+∞)上是增函数;
对于C,定义域为(0,+∞),是非奇非偶的函数;
对于D,定义域为R,并且为偶函数,但是在(0,+∞)上是减函数.
对于B,定义域为R,并且|-x|+1=|x|+1,是偶函数,并且在(0,+∞)上是增函数;
对于C,定义域为(0,+∞),是非奇非偶的函数;
对于D,定义域为R,并且为偶函数,但是在(0,+∞)上是减函数.
点评:本题考查了函数的单调性及奇偶性的判断;属于基础题.

练习册系列答案
相关题目
函数y=cos(
x+
)是( )
| 1 |
| 2 |
| π |
| 2 |
| A、周期为2π的偶函数 |
| B、周期为4π的奇函数 |
| C、周期为4π的偶函数 |
| D、周期为π的奇函数 |
已知直线ax+by-1=0(a>0,b>0)过圆x2+y2-4x-2y=0的圆心,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| 2b |
A、
| ||
B、
| ||
C、
| ||
D、
|
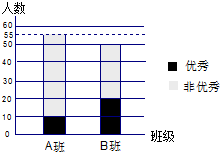 中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.
中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.