题目内容
已知f(2x+1)=3x-2且函数y=f(x)的图象过点(a,4),则a的值为 .
考点:函数的零点,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:由函数y=f(x)的图象过点(a,4)知,3x-2=4,a=2x+1,从而求解.
解答:
解:由题意,令3x-2=4,解得,x=2;
则a=2x+1=2×2+1=5,
故答案为:5.
则a=2x+1=2×2+1=5,
故答案为:5.
点评:本题考查了复合函数的相关性质,属于基础题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
在数列{an}中,a1=2,an+1=an+ln(1+
),则an=( )
| 1 |
| n |
| A、2+ln n |
| B、2+(n-1)ln n |
| C、2+n ln n |
| D、1+n+ln n |
由y=ex、x轴、y轴及直线x=2围成的封闭图形的面积为( )
| A、e2 |
| B、e2-1 |
| C、e2+1 |
| D、e2ln2-1 |
函数y=cos(
x+
)是( )
| 1 |
| 2 |
| π |
| 2 |
| A、周期为2π的偶函数 |
| B、周期为4π的奇函数 |
| C、周期为4π的偶函数 |
| D、周期为π的奇函数 |
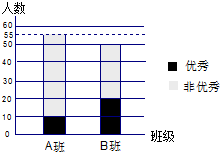 中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.
中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.