题目内容
12.已知函数f(x)=5x2+$\frac{a}{x}$+$\frac{1}{4}$(x>0),g(x)=lnx+4,曲线y=g(x)在点(1,4)处的切线与曲线y=f(x)相切.(1)求实数a的值;
(2)证明:当x≥0时,f(x)>g(x)
分析 (1)由g(x)=lnx+4,得g′(x)=$\frac{1}{x}$,由导数的几何意义得曲线在(1,4)处的切线方程为y=x+3,由f′(x)=10x-$\frac{a}{{x}^{2}}$,且函数f(x)=5x2+$\frac{a}{x}$+$\frac{1}{4}$(x>0)与y=x+3相切,能求出实数a的值.
(2)f(x)=5x2+$\frac{1}{x}$+$\frac{1}{4}$(x>0),设h(x)=f(x)-(x+3)=5x2+$\frac{1}{x}$-x-$\frac{11}{4}$,则h′(x)=10x-$\frac{1}{{x}^{2}}$-1=$\frac{10{x}^{3}-{x}^{2}-1}{x}$设m(x)=10x3-x2-1,则m′(x)=30x2-2x=2x(15x-1),由此利用导数性质能证明当x≥0时,f(x)>g(x).
解答 解:(1)由g(x)=lnx+4,得g′(x)=$\frac{1}{x}$,
y=g(x)在(1,4)处的切线斜率k=g′(1)=1,
则曲线在(1,4)处的切线方程y-4=(x-1),即y=x+3,
由函数f(x)=5x2+$\frac{a}{x}$+$\frac{1}{4}$(x>0),求导得,f′(x)=10x-$\frac{a}{{x}^{2}}$,
由函数f(x)=5x2+$\frac{a}{x}$+$\frac{1}{4}$(x>0)与y=x+3相切,
则设切点P(x0,5x02+$\frac{a}{{x}_{0}}$+$\frac{1}{4}$),则10x0-$\frac{a}{{{x}_{0}}^{2}}$=1,即a=10x03-x02,①
则在P处的切线方程:y-(5x02+$\frac{a}{{x}_{0}}$+$\frac{1}{4}$)=x-x0,
整理得:y=x+(5x02+$\frac{a}{{x}_{0}}$+$\frac{1}{4}$)-x0,则5x02+$\frac{a}{{x}_{0}}$+$\frac{1}{4}$-x0=3,②
由x>0,解得:x=$\frac{1}{2}$,a=1,
∴实数a的值为1;
(2)证明:由(1)可知:f(x)=5x2+$\frac{1}{x}$+$\frac{1}{4}$(x>0),
设h(x)=f(x)-(x+3)=5x2+$\frac{1}{x}$-x-$\frac{11}{4}$,
则h′(x)=10x-$\frac{1}{{x}^{2}}$-1=$\frac{10{x}^{3}-{x}^{2}-1}{x}$
设m(x)=10x3-x2-1,∴m′(x)=30x2-2x=2x(15x-1),
令m′(x)=0,解得x=$\frac{1}{15}$,
当x∈(0,$\frac{1}{15}$),m′(x)<0,函数递减,
当x∈($\frac{1}{15}$,+∞),m′(x)>0,函数递增,
∵m(0)=-1<0,m(1)=8>0,
∴?x0∈(0,1),使10x03-x02-1=0,∴10x02=$\frac{1+{{x}_{0}}^{2}}{{x}_{0}}$,
∴h(x)在(0,x0)上递减,在(x0,+∞)上递增,
∴h(x)min=h(x0)=$5{{x}_{0}}^{2}+\frac{1}{{x}_{0}}-{x}_{0}-\frac{11}{4}$
=$\frac{1}{2}({x}_{0}+\frac{1}{{x}_{0}})+\frac{1}{{x}_{0}}-{x}_{0}-\frac{11}{4}$
=$\frac{3}{2{x}_{0}}-\frac{{x}_{0}}{2}$-$\frac{1}{4}$>$\frac{3}{2}-\frac{1}{2}-\frac{1}{4}$>0,
∴f(x)>x+3,
设t(x)=x+3-ln(x+4),x>-4,则${t}^{'}(x)=1-\frac{1}{x+4}$=$\frac{x+3}{x+4}$,
由t′(x)>0,得x>-3,由t′(x)<0,得-4<x<-3,
∴t(x)的增区间是(-3,+∞),减区间是(-4,-3),
∴t(x)min=t(-3)=0,∴当x≥0时,ln(x+4)<x+3,
∴当x≥0时,f(x)>g(x).
点评 本题考查实数值的求法,考查不等式的证明,考查导数的性质及应用、导数的几何意义等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 优学名师名题系列答案
优学名师名题系列答案| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
(2)有多大点把握认为完成比赛与年龄是否有关?
附:下面的临界值表及公式供参考:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
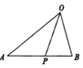 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
(1)根据以上数据建立一个2×2列联表;
(2)判断是否有95%的把握认为“性别与休闲方式”有关系.
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(Χ2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
| 支持 | 反对 | 总计 | |
| 男生 | 30 | ||
| 女生 | 25 | ||
| 总计 |
(2)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$
| P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.7069% | 3.841 | 6.635 | 7.879 | 10.828 |