题目内容
17.几何体三视图如图所示,则几何体的体积为( )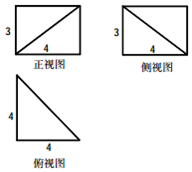
| A. | 32 | B. | 16 | C. | 8 | D. | 8$\sqrt{2}$ |
分析 先由三视图判断出几何体的形状及度量长度,然后利用柱体和锥体体积公式,可计算答案.
解答 解:由三视图得,该几何体为一个三棱柱切去一个同底同高的三棱锥所得的组合体,
它们的底面面积S=$\frac{1}{2}$×4×4=8,
高h=3,
故组合体的体积V=Sh-$\frac{1}{3}$Sh=$\frac{2}{3}$Sh=16,
故选:B.
点评 解决三视图的题目,关键是由三视图判断出几何体的形状及度量长度,然后利用几何体的面积及体积公式解决.

练习册系列答案
相关题目
12.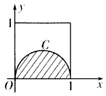 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
 如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )
如图正方形的曲线C是以1为直径的半圆,从区间[0,1]上取1600个随机数x1,x2,…,x800,y1,y2,…,y800,已知800个点(x1,y1),(x2,y2),…,(x800,y800)落在阴影部分阴影部分的个数为m,则m的估计值为( )| A. | 157 | B. | 314 | C. | 486 | D. | 628 |
9.已知函数$f(x)=ln({x+1})-\frac{ax}{1-x}({a∈R})$.
(1)当a=1时,求函数f(x)的单调区间;
(2)若-1<x<1时,均有f(x)≤0成立,求实数a的取值范围.
(1)当a=1时,求函数f(x)的单调区间;
(2)若-1<x<1时,均有f(x)≤0成立,求实数a的取值范围.
7.在△ABC中,角A,B,C的对边分别为a,b,c,若c=2,a2=b2+1,则acosB=( )
| A. | $\frac{5}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | 5 |
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°. 已知函数f(x)=|2x-1|-2|x-1|.
已知函数f(x)=|2x-1|-2|x-1|.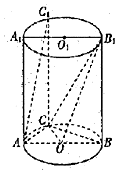 如图,在圆柱OO1中,矩形ABB1A1是过OO1的截面CC1是圆柱OO1的母线,AB=2,AA1=3,∠CAB=$\frac{π}{3}$.
如图,在圆柱OO1中,矩形ABB1A1是过OO1的截面CC1是圆柱OO1的母线,AB=2,AA1=3,∠CAB=$\frac{π}{3}$.