题目内容
16.已知f(x)=2xlnx,g(x)=-x2+ax-3.(1)求函数f(x)的单调区间;
(2)若存在x∈(0,+∞),使f(x)≤g(x)成立,求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题等价于a≥(2ln x+x+$\frac{3}{x}$)min,记h(x)=2ln x+x+$\frac{3}{x}$,x∈(0,+∞),根据函数的单调性判断即可.
解答 解:(1)f(x)的定义域为(0,+∞),f′(x)=2(ln x+1),
令f′(x)=0,得x=$\frac{1}{e}$,当x∈时,f′(x)<0,当x∈时,f′(x)>0,
所以f(x)在$\b\lc\(\rc\)(\a\vs4\al\co1(0,\frac{1}{e}))$上单调递减;在$\b\lc\(\rc\)(\a\vs4\al\co1(\frac{1}{e},+∞))$上单调递增.
(2)存在x∈(0,+∞),使f(x)≤g(x)成立,
即2xln x≤-x2+ax-3在x∈(0,+∞)能成立,
等价于a≥2ln x+x+$\frac{3}{x}$在x∈(0,+∞)能成立,
等价于a≥(2ln x+x+$\frac{3}{x}$)min.
记h(x)=2ln x+x+$\frac{3}{x}$,x∈(0,+∞),
则h′(x)=$\frac{2}{x}$+1-$\frac{3}{x2}$=$\frac{x2+2x-3}{x2}$=$\frac{?x+3??x-1?}{x2}$.
当x∈(0,1)时,h′(x)<0,
当x∈(1,+∞)时,h′(x)>0,
所以当x=1时,h(x)取最小值为4,故a≥4.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
5.若函数f(x)=(ax2+bx)ex的图象如图所示,则实数a,b的值可能为( )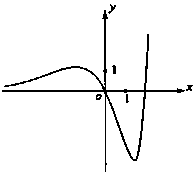

| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
4.若函数f(x)=a-$\frac{1}{{2}^{x}+1}$是奇函数,则实数a的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{3}$ |
1.设集合A={x|$\frac{x+1}{1-x}$>0},B={x|x+2≥0},则A∩B=( )
| A. | {x|-1<x<1} | B. | {x|x≥-2} | C. | {x|-2≤x<1} | D. | {x|-1<x≤2} |
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°. 已知函数f(x)=|2x-1|-2|x-1|.
已知函数f(x)=|2x-1|-2|x-1|.