题目内容
14. 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.(Ⅰ)若DE∥平面A1MC1,求$\frac{CE}{EB}$;
(Ⅱ)求直线BG和平面A1MC1所成角的余弦值.
分析 (Ⅰ)取BC中点N,连结MN,C1N,由已知得A1,M,N,C1四点共面,由已知条件推导出DE∥C1N,从而求出$\frac{CE}{EB}$.
(Ⅱ)连结B1M,由已知条件得四边形ABB1A1为矩形,B1C1与平面A1MC1所成的角为∠B1C1M,由此能求出直线BC和平面A1MC1所成的角的余弦值.
解答 解:(Ⅰ)取BC中点N,连结MN,C1N,…(1分)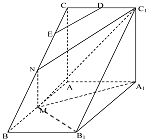
∵M,N分别为AB,CB中点
∴MN∥AC∥A1C1,
∴A1,M,N,C1四点共面,…(3分)
且平面BCC1B1∩平面A1MNC1=C1N,
又DE∩平面BCC1B1,
且DE∥平面A1MC1,∴DE∥C1N,
∵D为CC1的中点,∴E是CN的中点,…(5分)
∴$\frac{CE}{EB}$=$\frac{1}{3}$.…(6分)
(Ⅱ)连结B1M,…(7分)
因为三棱柱ABC-A1B1C1为直三棱柱,∴AA1⊥平面ABC,
∴AA1⊥AB,即四边形ABB1A1为矩形,且AB=2AA1,
∵M是AB的中点,∴B1M⊥A1M,
又A1C1⊥平面ABB1A1,
∴A1C1⊥B1M,从而B1M⊥平面A1MC1,…(9分)
∴MC1是B1C1在平面A1MC1内的射影,
∴B1C1与平面A1MC1所成的角为∠B1C1M,
又B1C1∥BC,
∴直线BC和平面A1MC1所成的角即B1C1与平面A1MC1所成的角…(10分)
设AB=2AA1=2,且三角形A1MC1是等腰三角形
∴A1M=A1C1=$\sqrt{2}$,则MC1=2,B1C1=$\sqrt{6}$,
∴cos∠B1C1M=$\frac{\sqrt{6}}{3}$,∴直线BC和平面A1MC1所成的角的余弦值为$\frac{\sqrt{6}}{3}$.…(12分)
点评 本题考查两条线段的比值的求法,考查角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
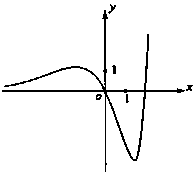
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |

| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{3}$ |
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.