题目内容
已知函数f(x)=2x+alnx,
(Ⅰ)若f(x)在(1,f(1))的切线为y=3x-1,求a;
(Ⅱ)若存在x∈[1,e],使不等式f(x)≤(a+3)x-
x2成立,求a的取值范围.
(Ⅰ)若f(x)在(1,f(1))的切线为y=3x-1,求a;
(Ⅱ)若存在x∈[1,e],使不等式f(x)≤(a+3)x-
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由已知得f′(x)=2+
,k=f′(1)=2+a=3,由此能求出a=1.
(Ⅱ)由已知得2x+alnx≤(a+3)x-
x2,a(x-lnx)≥
x2-x,从而a≥
,设g(x)=
,x∈[1,e],
由此利用导数性质能求出a≥-
.
| a |
| x |
(Ⅱ)由已知得2x+alnx≤(a+3)x-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| x-lnx |
| ||
| x-lnx |
由此利用导数性质能求出a≥-
| 1 |
| 2 |
解答:
解:(Ⅰ)∵f(x)=2x+alnx,
∴x>0,f(1)=2,
f′(x)=2+
,
∵f(x)在(1,f(1))的切线为y=3x-1,
∴k=f′(1)=2+a=3,
解得a=1.
(Ⅱ)∵存在x∈[1,e],使不等式f(x)≤(a+3)x-
x2成立,
∴2x+alnx≤(a+3)x-
x2,
∴a(x-lnx)≥
x2-x,
∵x∈[1,e],∴lnx≤1≤x,
且等号不能同时取到,∴lnx<x,即x-lnx>0,
∴a≥
,设g(x)=
,x∈[1,e],
∵g′(x)=
=
,
当x∈(1,e)时,x-1>0,lnx<1,
∴
x+1-lnx>0,
∴g′(x)>0,又∵g(x)在x=1和x=e处连续,
∴g(x)在x∈[1,e]时为增函数,因而g(x)≥g(1)=-
,
∴a≥-
.…(12分)
∴x>0,f(1)=2,
f′(x)=2+
| a |
| x |
∵f(x)在(1,f(1))的切线为y=3x-1,
∴k=f′(1)=2+a=3,
解得a=1.
(Ⅱ)∵存在x∈[1,e],使不等式f(x)≤(a+3)x-
| 1 |
| 2 |
∴2x+alnx≤(a+3)x-
| 1 |
| 2 |
∴a(x-lnx)≥
| 1 |
| 2 |
∵x∈[1,e],∴lnx≤1≤x,
且等号不能同时取到,∴lnx<x,即x-lnx>0,
∴a≥
| ||
| x-lnx |
| ||
| x-lnx |
∵g′(x)=
(x-1)(x-lnx)-(1-
| ||||
| (x-lnx)2 |
=
(x-1)(
| ||
| (x-lnx)2 |
当x∈(1,e)时,x-1>0,lnx<1,
∴
| 1 |
| 2 |
∴g′(x)>0,又∵g(x)在x=1和x=e处连续,
∴g(x)在x∈[1,e]时为增函数,因而g(x)≥g(1)=-
| 1 |
| 2 |
∴a≥-
| 1 |
| 2 |
点评:本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设向量a=(2,0),b=(1,1),则下列结论中正确的是( )
| A、|a|=|b| | ||
B、a=(2,0)•b=(1,1)=
| ||
| C、a∥b | ||
| D、(a-b)⊥b |
函数y=
的定义域为( )
| ||
| x-2 |
| A、{x|x≠2} |
| B、{x|x≥0且x≠2} |
| C、{x|x≥0} |
| D、{x|x≥1且x≠2} |
两个平面能把空间分成几个部分( )
| A、2或3 | B、3或4 |
| C、3 | D、2或4 |
某中学有学生270人(其中一年级108人,二、三年级各81人),将学生按一、二、三年级依次统一编号为1,2,…,270,现考虑选用简单随机抽样、分层抽样和系统抽样三种方案从中抽取10人参加某项调查,如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
| A、②、③都不能为系统抽样 |
| B、②、④都不能为分层抽样 |
| C、③、④都可能为系统抽样 |
| D、①、③都可能为分层抽样 |
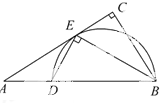 如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.
如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.