题目内容

设
a
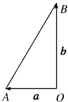
表示向西走10km，
b
表示向北走10
3
 km，则
a
-
b
表示（　　）
A、南偏西30°走20 km
B、北偏西30°走20 km
C、南偏东30°走20 km
D、北偏东30°走20 km
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：根据已知，求出
a
-
b
的模和∠OBA，即可得到
a
-
b
表示几何意义．
解答： 解：∵|
a
|=AO=10，|
b
|=BO=10
3
，
且＜
a
，
b
＞=90°，
则
a
-
b
=
BA
，
由勾股定理可得：|
BA
|=20，且∠OBA=30°，
故
a
-
b
表示：南偏西30°走20 km，
故选：A
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，属于基础题．
练习册系列答案
相关题目
在吸烟与患肺癌病这两个分类变量的计算中，下列说法正确的是（　　）
①若K2的观测值满足K2≥6.635，则我们有99%的把握认为吸烟与患肺癌病有关系，那么在100个吸烟的人中必有99个人患有肺癌病
②由独立性检验知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病
③从统计量中得知有99%的把握认为吸烟与患肺病有关系，是指有1%的可能性使得推断出现错误的是．
A、①③B、③C、②D、①
已知函数f（x）=log
1
2
cos
πx
3
，x∈（0，1），函数g（x）=asin（
π
6
x）-2a+2（a＞0），x∈（0，1）．若存在x1，x2∈（0，1），使得f（x1）=g（x2）成立，则实数a的取值范围是（　　）
A、（
4
3
，
3
2
）
B、（
2
3
，1）
C、（
1
2
，
4
3
）
D、（
1
3
，2）
设向量a=（2，0），b=（1，1），则下列结论中正确的是（　　）
A、|a|=|b|
B、a=（2，0）•b=（1，1）=
1
2
C、a∥b
D、（a-b）⊥b
若a=20.5，b=logπ3，c=log2sin
2π
5
，则a，b，c之间的大小关系是（　　）
A、c＞a＞b
B、a＞b＞c
C、b＞a＞c
D、b＞c＞a
下列命题中，正确的是（　　）
A、
a
=（-2，5）与
b
=（4，-10）方向相同
B、
a
=（4，10）与
b
（-2，-5）方向相反
C、
a
=（-3，1）与
b
=（-2，-5）方向相反
D、
a
=（2，4）与
b
=（-3，1）的夹角为锐角
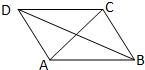如图平行四边形ABCD中，
AC
=（1，2），
BD
=（-3，2），则
AD
•
AC
=（　　）
A、1B、2C、3D、4
函数y=
ex-1
x-2
的定义域为（　　）
A、{x|x≠2}
B、{x|x≥0且x≠2}
C、{x|x≥0}
D、{x|x≥1且x≠2}
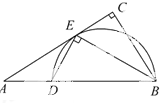如图，在Rt△ABC中，∠=90°，BE平分∠ABC，交AC于点E，点D在AB上，DE⊥EB．
（1）求证：AC是△BDE的外接圆的切线；
（2）若∠ABC=60°，AE=6，求EC的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网