Question

12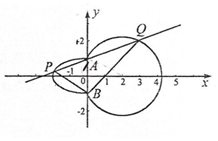．如图，曲线C由左半椭圆M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0，x≤0）和圆N：（x-2）²+y²=5在y轴右侧的部分连接而成，A，B是M与N的公共点，点P，Q（均异于点A，B）分别是M，N上的动点．
（1）若|PQ|的最大值为4+$\sqrt{5}$，求半椭圆M的方程；
（2）若直线PQ过点A，且$\overrightarrow{AQ}$+$\overrightarrow{AP}$=$\overrightarrow{0}$，$\overrightarrow{BP}$⊥$\overrightarrow{BQ}$，求半椭圆M的离心率．

Answer 1

分析 （1）A（0，1），B（0，-1），故b=1，|PQ|的最大值为4+$\sqrt{5}$=a+2+$\sqrt{5}$，解得a即可得出．
（2）设PQ方程：y=kx+1，与圆N的方程联立可得：（k²+1）x²+（2k-4）x=0，解得Q坐标．利用$\overrightarrow{AQ}$+$\overrightarrow{AP}$=$\overrightarrow{0}$，$\overrightarrow{AQ}$=（x_Q，y_Q-1）可得P的坐标．利用$\overrightarrow{BP}$⊥$\overrightarrow{BQ}$，可得$\overrightarrow{BP}•\overrightarrow{BQ}$=0，解得k．代入椭圆方程解得a²，即可得出．

解答 解：（1）A（0，1），B（0，-1），故b=1，|PQ|的最大值为4+$\sqrt{5}$=a+2+$\sqrt{5}$，解得a=2．
∴半椭圆M的方程为：$\frac{{x}^{2}}{4}$+y²=1（-2≤x≤0）．
（2）设PQ方程：y=kx+1，与圆N的方程联立可得：（k²+1）x²+（2k-4）x=0，
x_A+x_Q=$\frac{4-2k}{1+{k}^{2}}$，x_A=0，∴Q$（\frac{4-2k}{1+{k}^{2}}，\frac{-{k}^{2}+4k+1}{1+{k}^{2}}）$．∵$\overrightarrow{AQ}$+$\overrightarrow{AP}$=$\overrightarrow{0}$，$\overrightarrow{AQ}$=（x_Q，y_Q-1）
$\overrightarrow{AP}$=（x_P，y_P-1），∴x_P+x_Q=0，y_P+y_Q=2．
∴x_P=$\frac{2k-4}{1+{k}^{2}}$，y_P=$\frac{3{k}^{2}-4k+1}{1+{k}^{2}}$．
∵$\overrightarrow{BP}$⊥$\overrightarrow{BQ}$，∴$\overrightarrow{BP}•\overrightarrow{BQ}$=x_Px_Q+（y_P+1）（y_Q+1）=$\frac{-（2k-4）^{2}}{（1+{k}^{2}）^{2}}$+$\frac{（-{k}^{2}+4k+1）（3{k}^{2}-4k+1）}{（{k}^{2}+1）^{2}}$+2+1=（k²+1）（16k-12）=0，
解得k=$\frac{3}{4}$．故P$（-\frac{8}{5}，-\frac{1}{5}）$．代入椭圆方程可得：$\frac{64}{25{a}^{2}}$+$\frac{1}{25}$=1，解得a²=$\frac{8}{3}$．
∴半椭圆M的离心率e=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{10}}{4}$．

点评 本题考查了椭圆与圆的标准方程方程及其性质、向量坐标运算性质、向量垂直与数量积的关系、一元二次方程的根与系数的关系，考查了推理能力与计算能力，属于难题．