题目内容
在△ABC中，内角A，B，C所对的边分别是a，b，c.已知a＝2，c＝
，cosA＝－
.
(1)求sinC和b的值；
(2)求cos(2A＋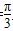
)的值．
(1)在△ABC中，
由cosA＝－，可得sinA＝
.
又由
＝
及a＝2，c＝，可得sinC＝
.
由a2＝b2＋c2－2bccosA，得b2＋b－2＝0，
因为b>0，故解得b＝1.
所以sinC＝，b＝1.
(2)由cosA＝－，sinA＝得，
cos2A＝2cos2A－1＝－
，
sin2A＝2sinAcosA＝－.
所以，cos(2A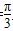＋)＝cos2Acos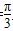－sin2Asin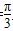
＝
.
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
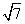，1,3} D．{－2－
、B＝60°，那么角A等于( )
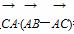＝18，求边c的长．
n mile B.
n mile
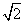n mile D．5
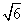n mile
B．λ>－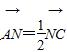
，BN与CM相交于点E，设
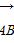＝a，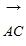
＝b，用基底a、b表示向量
＝________.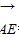