题目内容
已知A、B、C分别为△ABC的三边a、b、c所对的角,向量m=(sinA,sinB),n=(cosB,cosA),且m·n=sin2C.
(1)求角C的大小;
(2)若sinA、sinC、sinB成等差数列,且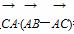 =18,求边c的长.
=18,求边c的长.
[解析] (1)m·n=sinA·cosB+sinB·cosA=sin(A+B).
在△ABC中,由于sin(A+B)=sinC.
∴m·n=sinC.
又∵m·n=sin2C,
∴sin2C=sinC,∴2sinCcosC=sinC.
又sinC≠0,所以cosC= .而0<C<π,因此C=
.而0<C<π,因此C=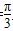 .
.
(2)由sinA,sinC,sinB成等差数列得,
2sinC=sinA+sinB,
由正弦定理得,2c=a+b.
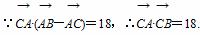 即abcosC=18,由(1)知,cosC=
即abcosC=18,由(1)知,cosC= ,所以ab=36.
,所以ab=36.
由余弦定理得,c2=a2+b2-2abcosC
=(a+b)2-3ab.
∴c2=4c2-3×36,∴c2=36.∴c=6.

练习册系列答案
相关题目

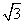 sinxcosx+cos2x+a.
sinxcosx+cos2x+a.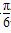 ,
,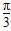 ]时,函数f(x)的最大值与最小值的和为
]时,函数f(x)的最大值与最小值的和为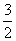 ,求f(x)的解析式;
,求f(x)的解析式;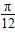 个单位,纵坐标不变,横坐标变为原来的2倍,再向下平移
个单位,纵坐标不变,横坐标变为原来的2倍,再向下平移 个单位,得到函数g(x)的图象,求g(x)的图象与x轴的正半轴、直线x=
个单位,得到函数g(x)的图象,求g(x)的图象与x轴的正半轴、直线x=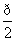 所围成图形的面积.
所围成图形的面积. ,则∠B=________.
,则∠B=________. bc且b=
bc且b= ,cosA=-
,cosA=- .
.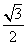 B.2-
B.2-
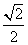
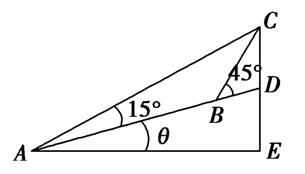
 ,则r+s的值是( )
,则r+s的值是( ) B.
B.
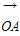 +
+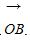 |=|
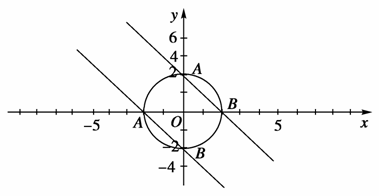
|=|
 或-
或-