题目内容
18.若直线4x-3y=0与圆x2+y2-2x+ay+1=0相切,则实数a的值为-1或4.分析 把圆的方程化为标准方程后,找出圆心坐标和圆的半径,然后根据直线与圆相切得到圆心到直线的距离等于圆的半径,列出关于a的方程,求出方程的解即可得到a的值.
解答 解:把圆的方程化为标准方程得:(x-1)2+(y+$\frac{a}{2}$)2=$\frac{{a}^{2}}{4}$,
所以圆心坐标为(1,-$\frac{a}{2}$),半径r=|$\frac{a}{2}$|,
由已知直线与圆相切,得到圆心到直线的距离d=$\frac{|4+\frac{3a}{2}|}{5}$=r=|$\frac{a}{2}$|,
解得a=-1或4.
故答案为:-1或4.
点评 此题考查学生灵活运用点到直线的距离公式化简求值,掌握直线与圆相切时满足的关系,是一道中档题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
8.设点O在△ABC内部且满足$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,现将一粒豆子撒在△ABC中,则豆子落在△OAB内的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
10.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的两个焦点分别为F1,F2,若椭圆上存在点P使得∠F1PF2是钝角,则椭圆离心率的取值范围是( )
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
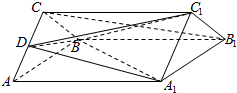 如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D
如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D