题目内容
8.设点O在△ABC内部且满足$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,现将一粒豆子撒在△ABC中,则豆子落在△OAB内的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
分析 根据三角形重心的性质,易得是△ABC的重心,由重心的性质,可得O到AB的距离为C到AB距离的$\frac{1}{3}$,可得△OAB的面积为△ABC的面积$\frac{1}{3}$,利用几何概型的意义求两个三角形的面积比即可分析可得答案
解答 解:根据题意,满足$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,则O是△ABC的重心,
由重心的性质,可得O到AB的距离为C到AB距离的$\frac{1}{3}$,
即△OAB的面积为△ABC的面积$\frac{1}{3}$,由几何概型公式可得豆子落在△OAB内的概率是$\frac{1}{3}$
故选:B.
点评 本题考查几何概型,将基本事件“几何化”,实际问题转化为数学问题,将随机事件的概率抽象为几何概型、向量关系式推出O的位置.

练习册系列答案
相关题目
13.已知m>n>0,x是m、n的等差中项,y是m、n的等比中项,则x,y的大小关系是( )
| A. | x>y | B. | x=y | ||
| C. | x<y | D. | 大小不确定,与m、n的取值有关 |
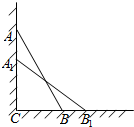 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.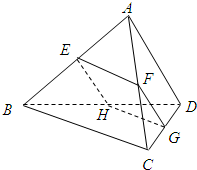 如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.
如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$. 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.