题目内容
6.若对任意的x>1,函数x+xln x≥k(3x-e)(其中e是白然对数的底数,e=2.71828…),则实数k的最大值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 整理不等式得$\frac{x+xlnx}{3x-e}$≥k恒成立,只需求出左式的最小值即可.构造函数,利用导函数求出函数的最小值.
解答 解:不等式可整理为
$\frac{x+xlnx}{3x-e}$≥k恒成立,
令f(x)=$\frac{x+xlnx}{3x-e}$,
f'(x)=$\frac{3x-2e-elnx}{(3x-e)^{2}}$,令h(x)=3x-2e-elnx,
∴h'(x)=3-$\frac{e}{x}$>0,则h(x)为增函数,
令h(x)=0得3x-2e-elnx=0,
∴x=e,
当x∈(1,e),f'(x)<0,f(x)递减,
当x∈(e,+∞),f'(x)>0,f(x)递增,
∴f(x)≥f(e)=1,
∴k≤1,
故选A.
点评 考查了恒成立问题的转化,构造函数,利用导函数判断函数的单调性.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.像“3,4,5”这样能够成直角三角形的数称为勾股数,又称为( )
| A. | 毕达哥拉斯数 | B. | 杨辉数 | C. | 拉格朗日恒等数 | D. | 三角数 |
15.复数z=1+2i的虚部是( )
| A. | -2i | B. | 2i | C. | -2 | D. | 2 |
 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,E为SC的中点,SD=AD.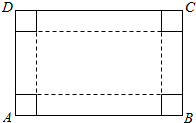 如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).
如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).