题目内容
3.已知矩阵A=$(\begin{array}{l}{2}&{3}\\{1}&{2}\end{array})$,矩阵B=$(\begin{array}{l}{2}&{0}&{1}\\{1}&{3}&{2}\end{array})$,C=$(\begin{array}{l}{2}\\{1}\\{-3}\end{array})$,(1)求AB;
(2)求(AB)C.
分析 (1)利用矩阵乘矩阵的运算法则求解.
(2)利用矩阵乘矩阵的运算法则求解.
解答 解:(1)∵矩阵A=$(\begin{array}{l}{2}&{3}\\{1}&{2}\end{array})$,矩阵B=$(\begin{array}{l}{2}&{0}&{1}\\{1}&{3}&{2}\end{array})$,
∴AB=$[\begin{array}{l}{2}&{3}\\{1}&{2}\end{array}]$$[\begin{array}{l}{2}&{0}&{1}\\{1}&{3}&{2}\end{array}]$=$[\begin{array}{l}{7}&{9}&{8}\\{4}&{6}&{5}\end{array}]$.
(2)(AB)C=$[\begin{array}{l}{7}&{9}&{8}\\{4}&{6}&{5}\end{array}]$$[\begin{array}{l}{2}\\{1}\\{-3}\end{array}]$=$[\begin{array}{l}{-1}\\{-1}\end{array}]$.
点评 本题考查矩阵的乘法的计算,是基础题,解题时要认真审题,注意矩阵乘矩阵的运算法则的合理运用.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
13.已知m>n>0,x是m、n的等差中项,y是m、n的等比中项,则x,y的大小关系是( )
| A. | x>y | B. | x=y | ||
| C. | x<y | D. | 大小不确定,与m、n的取值有关 |
8.在空间中,给出下列四个命题:
①平行于同一个平面的两条直线互相平行;
②垂直于同一个平面的两个平面互相平行;
③平行于同一条直线的两条直线互相平行;
④垂直于同一条直线的两条直线互相平行.
其中真命题的序号是( )
①平行于同一个平面的两条直线互相平行;
②垂直于同一个平面的两个平面互相平行;
③平行于同一条直线的两条直线互相平行;
④垂直于同一条直线的两条直线互相平行.
其中真命题的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
15.复数z=1+2i的虚部是( )
| A. | -2i | B. | 2i | C. | -2 | D. | 2 |
12. 某市乘坐出租车的收费办法如下:
某市乘坐出租车的收费办法如下:
不超过4千米的里程收费12元;超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费);当车程超过4千米时,另收燃油附加费1元.
相应系统收费的程序框图如图所示,其中x(单位:千米)为行驶里程,y(单位:元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )
 某市乘坐出租车的收费办法如下:
某市乘坐出租车的收费办法如下:不超过4千米的里程收费12元;超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费);当车程超过4千米时,另收燃油附加费1元.
相应系统收费的程序框图如图所示,其中x(单位:千米)为行驶里程,y(单位:元)为所收费用,用[x]表示不大于x的最大整数,则图中①处应填( )
| A. | $y=2[x-\frac{1}{2}]+4$ | B. | $y=2[x-\frac{1}{2}]+5$ | C. | $y=2[x+\frac{1}{2}]+4$ | D. | $y=2[x+\frac{1}{2}]+5$ |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(α>0,b>0)的左右焦点为F1,F2,|F1F2|=2$\sqrt{5}$,点P是双曲线右支上一点,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=10,在△PF1F2中,∠PF1F2的角平分线与另外两个角的外角平分线交于一点Q,Q点横坐标为4,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{15}}{3}$ |
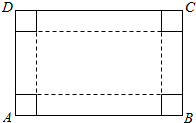 如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).
如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).