题目内容
8.在极坐标系中,过点$({2,\frac{3π}{2}})$且平行于极轴的直线的极坐标方程是ρsinθ=-2.分析 如图所示,在Rt△OPQ中,利用直角三角形的边角关系及诱导公式化简求解即可.
解答  解:如图所示
解:如图所示
在Rt△OPQ中,ρ=$\frac{2}{cos(θ-\frac{3π}{2})}$=$\frac{2}{-sinθ}$,
可化为ρsinθ=-2.
过点$({2,\frac{3π}{2}})$且平行于极轴的直线的极坐标方程是ρsinθ=-2.
故答案为:ρsinθ=-2.
点评 本题考查极坐标系的应用,熟练掌握直角三角形的边角关系及诱导公式是解题的关键.

练习册系列答案
相关题目
20.在△ABC中,若$\overrightarrow{AB}•(\overrightarrow{CA}+\overrightarrow{CB})=0$,且$\overrightarrow{BA}•\overrightarrow{BC}={\overrightarrow{BC}^2}$,则$\overrightarrow{AB}与\overrightarrow{BC}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
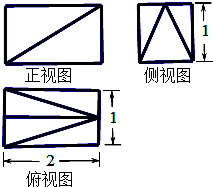
 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为直角三角形,则该三棱锥的体积等于( )
某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为直角三角形,则该三棱锥的体积等于( )