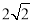题目内容
1.某几何体三视图如图所示,则该几何体的体积为$\frac{4}{3}$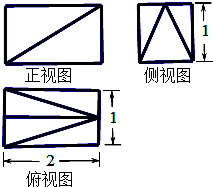
分析 由三视图可知几何体是由一个三棱柱与一个三棱锥组成,如图:几何体的体积是棱锥的体积与棱柱的体积的和.
解答 解:由三视图可知几何体是由一个三棱柱与一个三棱锥组成,如图:几何体的体积是棱锥的体积与棱柱的体积的和.
棱锥的体积为:$\frac{1}{3}×\frac{1}{2}×{1}^{2}×2$=$\frac{1}{3}$,
棱柱的体积为:$\frac{1}{2}×2×1×1$=1.
组合体的体积为:1+$\frac{1}{3}=\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了三棱柱与三棱锥三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.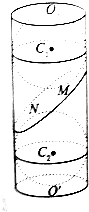 如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )
如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )
 如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )
如图,已知圆柱OO′的底面半径为12,与底面成β角(其中cosβ=$\frac{12}{13}$,sinβ=$\frac{5}{13}$)的截面α截圆柱所得的平面图形为椭圆,已知球C1,C2分别与圆柱的侧面、底面相切,与截面α相切于点M、N,在圆柱OO′的体积为( )| A. | 7500π | B. | 7200π | C. | 7800π | D. | 8100π |
16.等比数列{an}的首项为2,项数为奇数,其奇数项之和为$\frac{85}{32}$,偶数项之和为$\frac{21}{16}$,这个等比数列前n项的积为Tn(n≥2),则Tn的最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
9.积分$\int_0^1{{e^x}dx}$的值为( )
| A. | e | B. | e-1 | C. | 1 | D. | e2 |
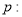 函数
函数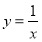 在定义域上为减函数,命题
在定义域上为减函数,命题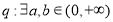 ,当
,当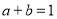 时,
时,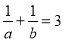 ,以下说法正确的是( )
,以下说法正确的是( )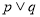 为真 B.
为真 B.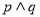 为真
为真 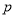 真
真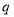 假 D.
假 D. 均假
均假 表示的平面区域为
表示的平面区域为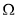 ,
,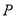 、
、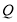 均为
均为 内一点,
内一点, 为坐标原点,
为坐标原点, ,则下列判断正确的是( )
,则下列判断正确的是( )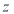 的最小值为
的最小值为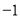 B.
B. 的最小值为
的最小值为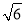
 的最大值为
的最大值为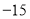 D.
D.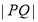 的最大值为
的最大值为