题目内容
15.(1)设函数f(x)=$\sqrt{|{x+1}|+|{x-2}|-a}$的定义域为R,试求a的取值范围;(2)已知实数x,y,z满足x+2y+3z=1,求x2+y2+z2的最小值.
分析 (1)利用绝对值不等式的性质可得:|x+1|+|x-2|≥|x+1-(x-2)|=3,即可得出;
(2)利用柯西不等式的性质即可得出.
解答 解:(1)由题设知,当x∈R时,恒有|x+1|+|x-2|-a≥0,
即|x+1|+|x-2|≥a,又|x+1|+|x-2|≥|x+1-(x-2)|=3,
∴a≤3.
(2)由柯西不等式(x2+y2+z2)(12+22+32)≥(x+2y+3z)2=1,
∴x2+y2+z2≥$\frac{1}{14}$,
当且仅当$\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$时,即x=$\frac{1}{14}$,y=$\frac{1}{7}$,z=$\frac{3}{14}$时,
x2+y2+z2的最小值为$\frac{1}{14}$.
点评 本题考查了绝对值不等式的性质、柯西不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
3.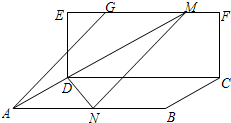 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-C的平面角的取值范围为( )
 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-C的平面角的取值范围为( )
| A. | [30°,45°] | B. | [45°,60°] | C. | [30°,90°) | D. | [60°,90°) |
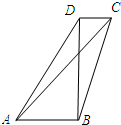 如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )
如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )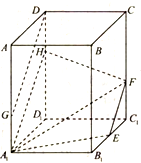 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.