题目内容
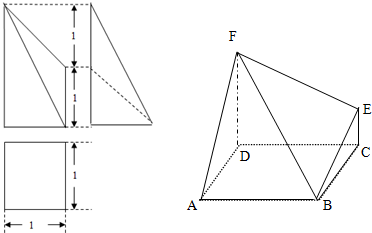
16. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为直角三角形,则该三棱锥的体积等于( )
某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为直角三角形,则该三棱锥的体积等于( )| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
分析 该几何体是一个三棱锥,底面是一个边长为2的等边三角形,后侧面也是一个边长为2的等边三角形且垂直底面,根据三棱锥的体积公式计算即可.
解答 解:该几何体是一个三棱锥,底面是一个边长为2的等边三角形,后侧面是一个边长为2的等边三角形,故该三棱锥的高为$\sqrt{3}$,
所以$V=\frac{1}{3}×(\frac{1}{2}×2×\sqrt{3})×\sqrt{3}=1$.
故选A
点评 本题考查了空间几何体的三视图及体积,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.积分$\int_0^1{{e^x}dx}$的值为( )
| A. | e | B. | e-1 | C. | 1 | D. | e2 |
3.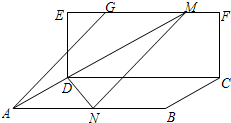 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-C的平面角的取值范围为( )
 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-C的平面角的取值范围为( )
| A. | [30°,45°] | B. | [45°,60°] | C. | [30°,90°) | D. | [60°,90°) |
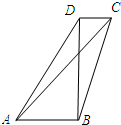 如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )
如图,在四边形ABCD中,|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4,$(|\overrightarrow{AB}|+|\overrightarrow{DC}|)|\overrightarrow{BD}$|=4,$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0,则$(\overrightarrow{AB}+\overrightarrow{DC})•\overrightarrow{AC}$的值为( )