题目内容
求函数y=2x+
的最大值和最小值．
| 1-2x |
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：根据解析式设t=
且t≥0，得2x=1-t2，代入解析式进行配方，根据t的范围、二次函数的性质，求出函数的最值．
| 1-2x |
解答：
解：设t=
，则t≥0，得2x=1-t2，
则原函数化为：y=-t2+t+1=-(t-
)2+
，
又t≥0，∴当t=
时，函数取到最大值是：
；
此函数没有最小值，
故函数的最大值是：
，无最小值．
| 1-2x |
则原函数化为：y=-t2+t+1=-(t-
| 1 |
| 2 |
| 5 |
| 4 |
又t≥0，∴当t=
| 1 |
| 2 |
| 5 |
| 4 |
此函数没有最小值，
故函数的最大值是：
| 5 |
| 4 |
点评：本题考查换元法求函数的最值，以及二次函数的性质，注意换元后求出未知数的范围．
练习册系列答案
中考解读考点精练系列答案
相关题目
已知椭圆的两个焦点为F1（-
，0），F2（
，0），P是此椭圆上的一点，且PF1⊥PF2，|PF1|•|PF2|=2，则该椭圆的方程是（ ）
| 5 |
| 5 |
A、
| ||
B、
| ||
C、x2+
| ||
D、x2+
|
a=0是复数a+bi（a，b∈R）为纯虚数的（ ）条件．
| A、充分 | B、必要 |
| C、充要 | D、非充分非必要 |
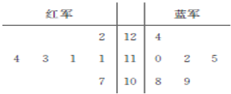解放军某部在实兵演练对抗比赛中，红、蓝两个小组均派6人参加实弹射击，其所得成绩的茎叶图如图所示．