题目内容
p:若关于x的方程sinx+cosx=m有实数解;q:f(x)=logmx在(0,+∞)为单调递增.当p、q有且仅有一个为真命题时,求m的取值范围.
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:对于命题p:由关于x的方程sinx+cosx=m有实数解,化为m=
sin(x+
),利用正弦函数的单调性即可得出;对于命题q:f(x)=logmx在(0,+∞)为单调递增.可得m>1.当p、q有且仅有一个为真命题时,分为以下两种情况:当p真q假时;当p假q真时,解出即可.
| 2 |
| π |
| 4 |
解答:
解:对于命题p:若关于x的方程sinx+cosx=m有实数解,则m=
sin(x+
),则m∈[-
,
];
对于命题q:f(x)=logmx在(0,+∞)为单调递增.则m>1.
当p、q有且仅有一个为真命题时,分为以下两种情况:
①当p真q假时,
,解得0<m<1;
②当p假q真时,
,解得m>
.
综上可知:当p真q假时,m∈(0,1);
②当p假q真时,m∈(
,+∞).
| 2 |
| π |
| 4 |
| 2 |
| 2 |
对于命题q:f(x)=logmx在(0,+∞)为单调递增.则m>1.
当p、q有且仅有一个为真命题时,分为以下两种情况:
①当p真q假时,
|
②当p假q真时,
|
| 2 |
综上可知:当p真q假时,m∈(0,1);
②当p假q真时,m∈(
| 2 |
点评:本题考查了三角函数和差化积、正弦函数的单调性、对数函数的单调性、分类讨论、命题的真假判断等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
函数f(x)=
sin2x+cos2x的一条对称轴方程是( )
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
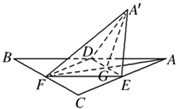 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形.其中正确的说法是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形.其中正确的说法是( )(1)动点A′在平面ABC上的射影在线段AF上
(2)恒有平面A′GF⊥平面BCED
(3)三棱锥A′-FED的体积有最大值
(4)异面直线A′E与BD不可能垂直.
| A、(1)(2)(3) |
| B、(1)(2)(4) |
| C、(2)(3)(4) |
| D、(1)(3)(4) |
 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,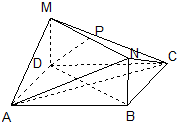 在如图所示的几何体中,四边形ABCD和BDMN都是矩形,且MD⊥平面ABCD,P是MN的中点.若AB=4,BC=3,MD=1,
在如图所示的几何体中,四边形ABCD和BDMN都是矩形,且MD⊥平面ABCD,P是MN的中点.若AB=4,BC=3,MD=1,