题目内容
已知集合A={x|2x2+7x-15<0},B={x|x2+ax+b≤0},若A∩B=∅,A∪B={x|-5<x≤2},则实数a,b的值分别是( )
| A、2,4 | ||
B、
| ||
C、
| ||
D、-
|
考点:集合的包含关系判断及应用
专题:集合
分析:首先,化简集合A,然后,结合条件A∩B=∅,A∪B={x|-5<x≤2},得到B={x|
≤x≤2},从而,
和2是方程x2+ax+b=0,的两根,进而,求得实数a,b的值.
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:由集合A得:
A={x|-5<x<
},
∵A∩B=∅,A∪B={x|-5<x≤2},
∴B={x|
≤x≤2},
∴
和2是方程x2+ax+b=0,的两根,
根据一元二次方程,根与系数的关系,得:
,
解得
,
故选:D.
A={x|-5<x<
| 3 |
| 2 |
∵A∩B=∅,A∪B={x|-5<x≤2},
∴B={x|
| 3 |
| 2 |
∴
| 3 |
| 2 |
根据一元二次方程,根与系数的关系,得:
|
解得
|
故选:D.
点评:本题重点考查集合的基本运算,属于容易题目.

练习册系列答案
相关题目
函数f(x)=
sin2x+cos2x的一条对称轴方程是( )
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
某几何体的三视图如图所示,则该几何体的体积为( )


A、4
| ||||
B、
| ||||
C、
| ||||
| D、3 |
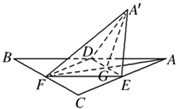 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形.其中正确的说法是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形.其中正确的说法是( )(1)动点A′在平面ABC上的射影在线段AF上
(2)恒有平面A′GF⊥平面BCED
(3)三棱锥A′-FED的体积有最大值
(4)异面直线A′E与BD不可能垂直.
| A、(1)(2)(3) |
| B、(1)(2)(4) |
| C、(2)(3)(4) |
| D、(1)(3)(4) |
 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,