题目内容
已知函数f(x)=ax-x2-lnx在(1,+∞)上是减函数,求g(x)=e2x-aex-1在[ln
,0]上的最小值.
| 1 |
| 3 |
考点:利用导数研究函数的单调性
专题:计算题,分类讨论,函数的性质及应用,导数的综合应用
分析:求出f(x)的导函数,据导函数的符号与函数单调性的关系,令导函数小于等于0恒成立,分离出a,利用函数的单调性求出函数的最小值,令a小于等于最小值即可得到a的范围.通过换元将函数g(x)转化为二次函数,通过对对称轴与定义域位置关系的讨论,分情况求出函数的最小值.
解答:
解:由于函数f(x)=ax-x2-lnx,导数f′(x)=a-2x-
,
∵f(x)在(1,+∞)上是减函数,
∴a-2x-
≤0在(1,+∞)上恒成立,
即a≤2x+
恒成立,
∴只需a≤(2x+
)min即可.
由于(2x+
)′=2-
>0,则(1,+∞)为增区间,则有a≤3.
再设ex=t,∵x∈[ln
,0],则t∈[
,1].
设h(t)=t2-at-1=(t-
)2-(1+
),
其对称轴t=
,由a≤3,则t=
≤
,
则当
≤
时,[
,1]为增区间,g(x)的最小值为h(
)=-
-
a;
当1≤
≤
时,[
,1]为减区间,g(x)的最小值为h(1)=-a;
当
<
<1时,g(x)的最小值为h(
)=-(1+
).
则g(x)的最小值为h(a)=
| 1 |
| x |
∵f(x)在(1,+∞)上是减函数,
∴a-2x-
| 1 |
| x |
即a≤2x+
| 1 |
| x |
∴只需a≤(2x+
| 1 |
| x |
由于(2x+
| 1 |
| x |
| 1 |
| x2 |
再设ex=t,∵x∈[ln
| 1 |
| 3 |
| 1 |
| 3 |
设h(t)=t2-at-1=(t-
| a |
| 2 |
| a2 |
| 4 |
其对称轴t=
| a |
| 2 |
| a |
| 2 |
| 3 |
| 2 |
则当
| a |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 9 |
| 1 |
| 3 |
当1≤
| a |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
当
| 1 |
| 3 |
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
则g(x)的最小值为h(a)=
|
点评:解决函数的单调性已知求参数的范围问题,常求出导函数,令导函数大于等于(或小于等于)0恒成立;解决不等式恒成立问题常分离参数转化为求函数的最值;通过换元法解题时,一定注意新变量的范围.

练习册系列答案
相关题目
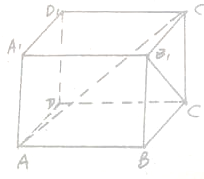 已知长方体AC1中,AB=BC=4cm,AA1=2cm,E,F分别为BB1和A1B1的中点,求:
已知长方体AC1中,AB=BC=4cm,AA1=2cm,E,F分别为BB1和A1B1的中点,求: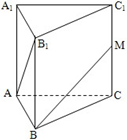 如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )
如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )