题目内容
判断函数y=
的奇偶性.
| 2sinx-1 |
考点:正弦函数的奇偶性,二倍角的余弦,余弦函数的奇偶性
专题:函数的性质及应用
分析:因为sinx≥
,故可求函数y=
的定义域为:
+2kπ≤x≤
+2kπ,k∈Z,由于定义域不关于原点对称,故函数y=
是非奇非偶函数.
| 1 |
| 2 |
| 2sinx-1 |
| π |
| 6 |
| 5π |
| 6 |
| 2sinx-1 |
解答:
解:依题意可得2sinx-1≥0即sinx≥
,
故函数y=
的定义域为:
+2kπ≤x≤
+2kπ,k∈Z
由于函数y=
的定义域不关于原点对称.
故函数y=
是非奇非偶函数.
| 1 |
| 2 |
故函数y=
| 2sinx-1 |
| π |
| 6 |
| 5π |
| 6 |
由于函数y=
| 2sinx-1 |
故函数y=
| 2sinx-1 |
点评:本题主要考察了函数的性质及应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
复数满足在z(1-i)=2i,则复数Z的实部和虚部只差为( )
| A、-2 | B、2 | C、1 | D、0 |
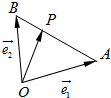 设
设| OA |
| e1 |
| OB |
| e2 |
| e1 |
| e2 |
| OP |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|