题目内容
已知函数f(x)=x+
+b(x≠0).,其中a,b∈R
(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=3x+1,求函数f(x)的解析式;
(2)当a>0时,求函数f(x)的单调区间.
| a |
| x |
(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=3x+1,求函数f(x)的解析式;
(2)当a>0时,求函数f(x)的单调区间.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)求出函数的导函数,由函数在x=2处的导数值得到a的值,再由点在直线上得到b的值,则函数解析式可求;
(2)由导函数等于0求得导函数的零点,利用导函数的零点对定义域分段,结合导函数在不同区间段内的符号得到函数的单调性.
(2)由导函数等于0求得导函数的零点,利用导函数的零点对定义域分段,结合导函数在不同区间段内的符号得到函数的单调性.
解答:
解:(1)由f(x)=x+
+b(x≠0),得
f′(x)=1-
,由导数的几何意义得f'(2)=3,于是a=-8,
由切点P(2,f(2))在直线y=3x+1上可得-2+b=7,解得b=9,
∴函数f(x)的解析式为f(x)=x-
+9;
(2)f′(x)=1-
,当a>0时,令f'(x)=0,解得x=±
,
当x变化时,f'(x),f(x)的变化情况如下表:
∴f(x)在(-∞,-
),(
,+∞)上是增函数,在(-
,0),(0,
)上是减函数.
| a |
| x |
f′(x)=1-
| a |
| x2 |
由切点P(2,f(2))在直线y=3x+1上可得-2+b=7,解得b=9,
∴函数f(x)的解析式为f(x)=x-
| 8 |
| x |
(2)f′(x)=1-
| a |
| x2 |
| a |
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,-
| -
| (-
| (0,
|
| (
| ||||||||||||
| f'(x) | + | 0 | - | - | 0 | + | ||||||||||||
| f(x) | 极大值 | 极小值 |
| a |
| a |
| a |
| a |
点评:本题考查了利用导数求过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
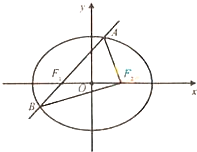 如图,椭圆E:
如图,椭圆E: