题目内容
设点M是等腰直角三角形ABC的底边AB的中点，P是直线AB上任意一点，PE⊥AC，E为垂足，PF⊥BC，F为垂足．求证：（1）|ME|=|MF|；
（2）ME⊥MF．
（2）ME⊥MF．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：建立平面直角坐标系C-xy，设AC=2，得到M，E，F，的坐标，利用向量的模以及向量垂直的性质解答．
解答：
解：建立平面直角坐标系C-xy，设AC=2，P在AB上，
所以设P（a，2-a），由题意，M（1，1），E（0.2-a），F（a，0），
所以
=（-1，1-a），
=（a-1，-1），
所以|
|=
，|
|=
，
所以（1）|ME|=|MF|；
（2）
•
=-a+1-1+a=0，
所以ME⊥MF．
所以设P（a，2-a），由题意，M（1，1），E（0.2-a），F（a，0），所以
| ME |
| MF |
所以|
| ME |
| 1+(a-1)2 |
| MF |
| (a-1)2+1 |
所以（1）|ME|=|MF|；
（2）
| ME |
| MF |
所以ME⊥MF．
点评：本题考查了利用向量证明相等长度相等以及直线垂直的问题，体现了向量的工具性．
练习册系列答案
阅读快车系列答案
相关题目
已知sin（-α）=
，α∈（-
，0），则tanα等于（ ）
2
| ||
| 3 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、2
| ||||
D、-2
|
如果执行如图所示的程序框图，输入x=6，则输出的y值为（ ）
| A、2 | ||
| B、0 | ||
| C、-1 | ||
D、-
|
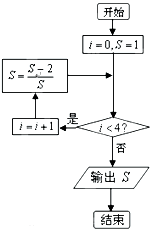
执行如图所示的程序框图，输出的S值为 （ ）
| A、-1 | ||
| B、3 | ||
C、
| ||
| D、-5 |