题目内容
10.若关于x的不等式x2-2ax-8a2<0的解集为(x1,x2),且x2-x1=15,则a=( )| A. | $\frac{5}{2}$ | B. | $-\frac{5}{2}$ | C. | $±\frac{15}{4}$ | D. | $±\frac{5}{2}$ |
分析 利用不等式的解集以及根与系数的关系得到两根关系式,再与已知条件化简求解a的值.
解答 解:关于x的不等式x2-2ax-8a2<0的解集为(x1,x2),
所以x1+x2=2a…①,
x1•x2=-8a2…②,
又x2-x1=15…③,
①2-4×②可得(x2-x1)2=36a2,
代入③可得,152=36a2,
解得a=±$\frac{5}{2}$.
故选:D.
点评 本题考查了一元二次不等式的解法与应用问题,是基础题.

练习册系列答案
相关题目
5. 如图,矩形ADFE,矩形CDFG,正方形ABCD两两垂直,且AB=2,若线段DE上存在点P使得GP⊥BP,则边CG长度的最小值为 ( )
如图,矩形ADFE,矩形CDFG,正方形ABCD两两垂直,且AB=2,若线段DE上存在点P使得GP⊥BP,则边CG长度的最小值为 ( )
 如图,矩形ADFE,矩形CDFG,正方形ABCD两两垂直,且AB=2,若线段DE上存在点P使得GP⊥BP,则边CG长度的最小值为 ( )
如图,矩形ADFE,矩形CDFG,正方形ABCD两两垂直,且AB=2,若线段DE上存在点P使得GP⊥BP,则边CG长度的最小值为 ( )| A. | 4 | B. | $4\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
19.端午节放假,甲回老家过节的概率为$\frac{1}{3}$,乙、丙回老家过节的概率分别为$\frac{1}{4}$,$\frac{1}{5}$.假定三人的行动相互之间没有影响,那么这段时间内至少1人回老家过节的概率为( )
| A. | $\frac{59}{60}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{60}$ |
20.cos45°cos15°+sin15°sin45°的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
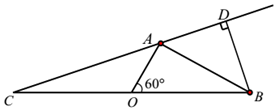 随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;
随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;