题目内容
已知点O是锐角△ABC的外心，AB=8，AC=12，A=
．若
=x
+y
，则6x+9y= ．
| π |
| 3 |
| AO |
| AB |
| AC |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，过点O分别作OD⊥AB，OE⊥AC，垂足分别为D，E．可得D，E分别为AB，AC的中点．可得
•
=
2，
•
=
2．由A=
，可得
•
．对
=x
+y
，两边分别与
，
作数量积即可得出．
| AO |
| AB |
| 1 |
| 2 |
| AB |
| AO |
| AC |
| 1 |
| 2 |
| AC |
| π |
| 3 |
| AB |
| AC |
| AO |
| AB |
| AC |
| AB |
| AC |
解答：
解：如图所示，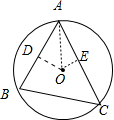
过点O分别作OD⊥AB，OE⊥AC，垂足分别为D，E．
则D，E分别为AB，AC的中点，
∴
•
=
2=
×82=32．
•
=
2=
×122=72．
∵A=
．
∴
•
=8×12×cos
=48．
∵
=x
+y
，
∴
•
=x
2+y
•
，
•
=x
•
+y
2，
化为32=64x+48y，72=48x+144y，
联立解得x=
，y=
．
∴6x+9y=5．
故答案为：5．
过点O分别作OD⊥AB，OE⊥AC，垂足分别为D，E．
则D，E分别为AB，AC的中点，
∴
| AO |
| AB |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AO |
| AC |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
∵A=
| π |
| 3 |
∴
| AB |
| AC |
| π |
| 3 |
∵
| AO |
| AB |
| AC |
∴
| AO |
| AB |
| AB |
| AC |
| AB |
| AO |
| AC |
| AB |
| AC |
| AC |
化为32=64x+48y，72=48x+144y，
联立解得x=
| 1 |
| 6 |
| 4 |
| 9 |
∴6x+9y=5．
故答案为：5．
点评：本题考查了向量数量积运算性质、三角形外心性质、垂经定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
长方体ABCD-A1B1C1D1中对角线AC1与平面ABCD、平面ABB1A1、平面AA1D1D上射影所成角分别为θ1、θ2，θ3，求cos2θ1+设函数f（x）=
x3+
ax2+2bx+c，f（x）在x=x1处取得极大值，在x=x2处取得极小值，且x1∈（0，1），x2∈（1，2），则
的取值范围为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
| A、（1，4） | ||||
B、（
| ||||
C、（
| ||||
D、（
|
在空间四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，对角线AC=BD=2，且AC⊥BD，则四边形EFGH的面积为
如图，直三棱柱ABC-A1B1C1中，AB=AC=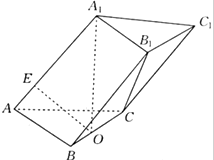
已知在三棱柱ABC-A1B1C1中，底面ABC为正三角形，A1在底面ABC上的射影是棱BC的中点O，OE⊥AA1于E点．