题目内容
某校举行“中国梦,我的梦”大型演讲比赛,分成高一,高二,高三三个组别共120人各组别中男女学生人数如下表:
已知在全体参赛学生中随机抽取1名男生,该男生是高一组合高二组的概率分别是0.2和0.15.
(1)求a,b,c的值;
(2)为了了解参赛学生的综合素质,现在三个年级的参数学生中按1:20的比例抽取选手进行综合素质测评,在选取的6个人中,随机抽取2人进行面试,求两名选手分别来自两个年级的概率.
| 高一 | 高二 | 高三 | |
| 男 | a | c | 5 |
| 女 | B | 22 | 15 |
(1)求a,b,c的值;
(2)为了了解参赛学生的综合素质,现在三个年级的参数学生中按1:20的比例抽取选手进行综合素质测评,在选取的6个人中,随机抽取2人进行面试,求两名选手分别来自两个年级的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)用概率×样本容量=频数,即可求出a,b,c的值;
(2)先求出各年级要抽取的人数,再根据古典概型的概率公司,即可得到结论.
(2)先求出各年级要抽取的人数,再根据古典概型的概率公司,即可得到结论.
解答:
解:(1)∵随机抽取1名男生,该男生是高一组合高二组的概率分别是0.2和0.15.
∴a=0.2×120=24,c=0.15×120=18,b=120-(24+18+5+22+15)=36
(2)高一年级的抽取的人数为:
×(24+36)=3人,记作a,b,c,
高二年级的抽取的人数为:
×(18+22)=2人,记作1,2,
高三年级的抽取的人数为:
×(5+15)=1人,记作m,
从中任取2个的基本事件为(a,b),(a,c),(a,1),(a,2),(a,m),(b,c),(b,1),(b,2),(b,m),(c,1),(c,2),(c,m),(1,2),(1,m),(2,m)共15个.
两名选手分别来自两个年级的基本事件有(a,1),(a,2),(a,m),(b,1),(b,2),(b,m),(c,1),(c,2),(c,m),(1,m),(2,m),共11个,
∴两名选手分别来自两个年级的概率P=
.
∴a=0.2×120=24,c=0.15×120=18,b=120-(24+18+5+22+15)=36
(2)高一年级的抽取的人数为:
| 1 |
| 20 |
高二年级的抽取的人数为:
| 1 |
| 20 |
高三年级的抽取的人数为:
| 1 |
| 20 |
从中任取2个的基本事件为(a,b),(a,c),(a,1),(a,2),(a,m),(b,c),(b,1),(b,2),(b,m),(c,1),(c,2),(c,m),(1,2),(1,m),(2,m)共15个.
两名选手分别来自两个年级的基本事件有(a,1),(a,2),(a,m),(b,1),(b,2),(b,m),(c,1),(c,2),(c,m),(1,m),(2,m),共11个,
∴两名选手分别来自两个年级的概率P=
| 11 |
| 15 |
点评:本题主要考查分层抽样的应用,以及古典概率的计算,利用列举法是解决本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
若a>0且a≠1,b>0,则“logab>0”是“(a一1)(b一1)>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设a,b,m为整数(m>0),若a和b被m除得的余数相同,则称a和b对m同余记为a≡b(bmodm),已知a=1+C201+C2022+C20322+…+C2020219,a≡b(bmod10),则b的值可以是( )
| A、2015 | B、2013 |
| C、2011 | D、2009 |
设函数f(x)=
x3+
ax2+2bx+c,f(x)在x=x1处取得极大值,在x=x2处取得极小值,且x1∈(0,1),x2∈(1,2),则
的取值范围为( )
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
| A、(1,4) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
 长方体ABCD-A1B1C1D1中对角线AC1与平面ABCD、平面ABB1A1、平面AA1D1D上射影所成角分别为θ1、θ2,θ3,求cos2θ1+
长方体ABCD-A1B1C1D1中对角线AC1与平面ABCD、平面ABB1A1、平面AA1D1D上射影所成角分别为θ1、θ2,θ3,求cos2θ1+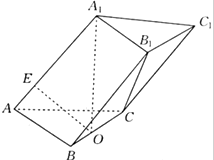 已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.
已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.